Algebra Chapter 1 Review

The material in this lesson is a review of previous algebra or pre-calculus courses. You
should be able to work through this material at a fairly rapid pace. If you find that much of
it is unfamiliar, or difficult, then you should consider reviewing at greater length. Any
college algebra text should have material similar to this lesson. At the University of Kansas,
the current text is College Algebra by Sullivan.

PART 1

By the end of this part of lesson 1, you should be able to
• distinguish between open, closed, and half-open intervals;
• understand and evaluate expressions involving absolute value; and
• work with exponents, including negative exponents and radical exponents , using the
Laws of Exponents.

Reading Assignment: Section 1.1 of Chapter 1

Notes and Comments

1. The symbol for absolute value is universal. Pay special attention to the definition of
the absolute value in the first highlighted box on page 6 of the text. The Absolute
Value Properties listed in the second highlighted box on page 6 are also very
important. Be sure to go over Example 3 at the bottom of page 6.

2. The Laws of Exponents (text, page 8; Table 1.4) have all the rules that you will need
when dealing with either integer or fractional exponents. It is important to remember
that an exponent is only attached to the obvious base; 2t² is not the same as

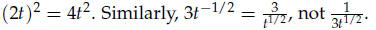
3. The connection between nth roots of a number and fractional exponents is a very
important one (page 8; Table 1.3). You should be able to use these two concepts
interchangeably.

4. The distinction between multiplying or dividing two exponential expressions to the
same base—Laws 1 and 2—and taking powers—Law 3—is important. Multiplying
two exponential powers to the same base turns into addition or subtraction of
exponents, while raising an exponential to a power requires a product or division of
exponents.

5. Be careful when applying the Laws of Exponents. The exponent does NOT satisfy the
distributive property . Thus, to multiply (a + b)ⁿ one must use the binomial expansion
to expand this expression .

Practice Assignment
Section 1.1: Exercises 3, 7, 15, 19, 23, 25, 39, 41, 49, 55, 77, 81, 111, 113, 115, 119.

PART 2

By the end of this part of lesson 1, you should be able to

• multiply and factor algebraic expressions, especially expressions involving
polynomials;
• use the Quadratic Formula to find the roots of polynomials of degree two; and
• simplify algebraic expressions (which may involve all arithmetic operations) and
arrive at a single fraction involving no negative exponents, and no common factors
between the numerator and the denominator.

Reading Assignment: Section 1.2 of Chapter 1

Notes and Comments

1. Multiplication of algebraic expressions is accomplished, in general, by using the
distributive rule illustrated in Example 2 (text, page 13). This method will always
provide the product, although there are some situations where a commonly used
product has a particular form; see Table 1.5 (page 13).

2. Factoring is the operation that attempts to un-multiply. This type of operation is
always more difficult than multiplication; see Table 1.6 (page 15). Factoring cannot
always be accomplished. Probably the best way to start is to attempt to group the
monomials so that a common factor can be identified. Then, using the distributive law
in reverse, the original expression can be written as a product.

3. A root, sometimes called a zero, of a polynomial p is a number a such that p(a) = 0.
The roots of a polynomial are very difficult to find in general, and the problem of
finding roots is one that goes back to ancient Egypt and Mesopotamia. The
Babylonians and the Greeks could find roots of polynomials for all polynomials of
degree 1 and 2, but it was in the fourteenth century that roots of polynomials of degree
3 and 4 could be solved.

4. The Quadratic Formula gives a method for solving all polynomials of degree 2. This
formula was known by the Greek mathematicians of the B.C. era. While it may be
possible to solve such a polynomial by factoring and then applying the fact that a
product of real numbers is equal to zero if and only if at least one of the real numbers
is equal to zero, the Quadratic Formula gives a sure-fire and quick method for finding
the roots of a second degree polynomial.

5. Doing addition and subtraction with rational expressions (quotients of polynomials) is
always difficult. You must remember that these operations can only be accomplished
by first finding a common denominator, just as when trying to add or subtract rational
numbers. The explicit rules for this are in Table 1.8 (page 19). In contrast,
multiplication and division are relatively easy to perform. When in doubt, perform the
desired operations with rational numbers and compare. The rules for multiplying or
dividing are in Table 1.7 (page 19).

6. Sometimes an algebraic expression will contain several rational expressions, together
with some of the arithmetic operations . The process for dealing with such expressions
is the same as the process when rational numbers replace the rational expressions. In
example 10a (page 20), the problem is to find the quotient of two expressions. The only
way we can simplify a quotient is to get both the numerator and denominator in the
form of rational expressions and then use Table 1.7. In example 10b, we first need to
eliminate the negative exponents, and then proceed in a manner similar to 10a.

7. Cancellation between terms in the numerator and denominator can be very tricky. The
best way to determine whether cancellation can occur is by factoring both the
numerator and denominator before canceling. Cancellation can only occur if there are
common factors in both the numerator and denominator. See Example 8 on page 19 of
your text.

Practice Assignment

Section 1.2: Exercises 15, 19, 37, 41, 43, 49, 57, 63, 67, 73, 77, 81, 85, 87.

PART 3

By the end of this part of lesson 1 you should be able to
• compute the distance between two points;
• find the slope of a line ; and
• use the point-slope form to find the equation of a straight line.

Reading Assignment: Sections 1.3 and 1.4 of Chapter 1

Notes and Comments

1. Every point in the plane can be associated with a pair of real numbers and, conversely,
every pair of real numbers can be associated with a point in the plane. It is this
association—both ways—that allows algebra and geometry to flourish together: a
geometric concept can be given an algebraic interpretation, and an algebraic
expression can be associated with a geometric figure in the Cartesian plane. (The word
Cartesian is in honor of Rene Descartes, who with Pierre Fermat invented analytic
geometry.)

2. The Euclidean, or Cartesian, plane arises from having two intersecting number lines.
Their point of intersection is called the origin, and is denoted by O. Since the two lines
are number lines, each has a scale of units, although the scales are not necessarily the
same on both lines. Whenever we work with analytic geometry, for example in
drawing graphs , these scales must be clearly denoted. There are a few conventions
that have arisen concerning these number lines. For example, the number lines
intersect in a right angle; one horizontal—called the x-axis—and the other
vertical—called the y-axis. On the x-axis, positive reals are displayed to the right,
negatives to the left, while on the y-axis, positives go up and negatives down. Because
the x-axis and y-axis intersect at right angles to each other, we can use the Pythagorean
theorem in order to compute the distance between any two points. The reason for this
is that any vertical line and any horizontal line must also intersect in right angles.
Therefore, the line connecting the two points, together with a line parallel to the x-axis
and another parallel to the y-axis, form a right-angle triangle. (See Figure 1.7, page 25.)

3. Every line in the Euclidean plane, except vertical lines, has a slope. This slope is
computed by selecting two points on the line and using Equation 3 on page 33. Note
that it does not matter what two points you choose; the slope will always be the same.
There are two important slopes that you should remember. The slope of a vertical line
is undefined. Why? Horizontal lines have slopes equal to zero.

4. One of the two parts of calculus, differential calculus, deals with tangents to the graph
of a function. In the situations we will encounter, we will be given a point on the
graph and the slope of the tangent line. Thus, while there are several formulas for
determining the equation for a (tangent) line, the point-slope form is the most
important and you should use this form when doing the exercises.

5. Observe that in the distance formula, it is unimportant whether we use (a − b) or
(b − a) in computing the distance, but in computing the slope, confusing the
designation of the first versus the second point may result in an error in the sign of the
slope . Thus, the slope of the line through the points (2, 4) and (−3, 6) is given by

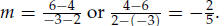
6. Lines with positive slopes will rise from left to right, while lines with negative slopes
will fall from left to right. Parallel lines have equal slopes and two lines that are
perpendicular (intersect at right angles) will have slopes such that their product equals
(−1) (page 37).

7. In the slope intercept form y = mx + b, m is the slope and the point (0, b), is the
y-intercept—the point where the line intersects the y-axis. If the equation is given in
this form, or can be algebraically manipulated to get this form, then the slope of the
line will be given by the coefficient of x. However, it is crucial that the equation be
written so that the coefficient of y equals 1.

Practice Assignment
Section 1.3: Exercises 21, 23, 25, 27, 29, 35, 39.
Section 1.4: Exercises 13, 15, 17, 23, 27, 41, 51, 53, 69, 71.

Written Assigment 1
Section 1.1: Exercises 26, 56, 82, 90, 114, 116.
Section 1.2: Exercises 6, 10, 42, 58, 74, 84.
Section 1.3: Exercises 26, 28, 30, 34, 36, 38.
Section 1.4: Exercises 14, 16, 18, 42, 54, 70, 76.

Don’t forget:

• If an exercise asks you to graph a particular function, this graph should be included as
part of the solution to the exercise.
• Every graph must have a scale of units clearly marked on both axes.
• Be sure to show all necessary work, or explain completely the process used to find the
answer to an exercise.
• Answers obtained by using a calculator must be correct to three (3) decimal places .
• Be sure to include an Independent Study cover sheet with your assignment.