The California Mathematics Content Standards

Introduction
to Grades Eight
Through Twelve

The standards for grades eight through
twelve are organized differently from those
for kindergarten through grade seven. In
this section strands are not used for
organizational purposes as they are in the
elementary grades because the mathematics
studied in grades eight through twelve
falls naturally under discipline headings:
algebra, geometry, and so forth. Many
schools teach this material in traditional
courses; others teach it in an integrated
fashion. To allow local educational
agencies and teachers flexibility in teaching
the material, the standards for grades
eight through twelve do not mandate that
a particular discipline be initiated and
completed in a single grade. The core
content of these subjects must be covered;
students are expected to achieve the
standards however these subjects are
sequenced.

Standards are provided for Algebra I ,
geometry, Algebra II, trigonometry ,
mathematical analysis , linear algebra ,
probability and statistics, advanced
placement probability and statistics, and
calculus. Many of the more advanced
subjects are not taught in every middle
school or high school. Moreover, schools
and districts have different ways of
combining the subject matter in these
various disciplines. For example, many
schools combine some trigonometry ,
mathematical analysis , and linear algebra
to form a precalculus course . Some
districts prefer offering trigonometry
content with Algebra II.

Table 1, “Mathematics Disciplines, by
Grade Level,” reflects typical grade-level
groupings of these disciplines in both
integrated and traditional curricula. The
lightly shaded region reflects the minimum
requirement for mastery by all
students. The dark shaded region depicts
content that is typically considered elective
but that should also be mastered by
students who complete the other disciplines
in the lower grade levels and
continue the study of mathematics.

Many other combinations of these
advanced subjects into courses are possible.
What is described in this section are
standards for the academic content by
discipline; this document does not endorse
a particular choice of structure for courses
or a particular method of teaching the
mathematical content.

When students delve deeply into
mathematics, they gain not only conceptual
understanding of mathematical
principles but also knowledge of, and
experience with, pure reasoning. One of
the most important goals of mathematics
is to teach students logical reasoning . The
logical reasoning inherent in the study of
mathematics allows for applications to a
broad range of situations in which answers
to practical problems can be found with
accuracy.

By grade eight, students’ mathematical
sensitivity should be sharpened. Students
need to start perceiving logical subtleties
and appreciate the need for sound mathematical
arguments before making
conclusions. As students progress in the
study of mathematics, they learn to
distinguish between inductive and deductive
reasoning; understand the meaning of
logical implication; test general assertions;

Table 1. Mathematics Disciplines, by Grade Level

	Grades
Disciplines	Eight	Nine	Ten	Eleven	Twelve
Algebra I
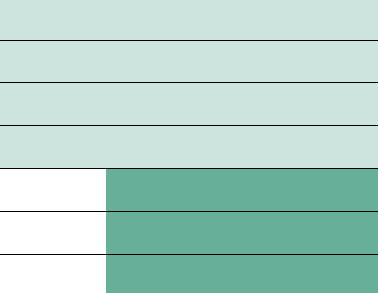Geometry
Algebra II
Probability and Statistics
Trigonometry
Linear Algebra
Mathematical Analysis
Advanced Placement Probability and Statistics
Calculus

realize that one counterexample is enough
to show that a general assertion is false;
understand conceptually that although a
general assertion is true in a few cases, it is
not true in all cases; distinguish between
something being proven and a mere
plausibility argument; and identify logical
errors in chains of reasoning.

Mathematical reasoning and conceptual
understanding are not separate from
content; they are intrinsic to the mathematical
discipline students master at
more advanced levels.