The Major Topics of School Algebra
The following extended discussion of The Major Topics
of School Algebra was
written by us in 2007 for the deliberations of the Conceptual Knowledge and
Skills
Task Group of the National Mathematics Advisory Panel. An abbreviated version
now appears in Section V, Sub-section A, of the Task Group’s report on
Conceptual
Knowledge . We believe this more elaborate version can still serve to round
off the discussion in the report itself.
Symbols and Expressions
• Polynomial expressions
• Rational expressions
• Arithmetic and finite geometric series
Linear Equations
• Real numbers as points on the number line
• Linear equations and their graphs
• Solving problems with linear equations
• Linear inequalities and their graphs
• Graphing and solving systems of simultaneous linear equations
Quadratic Equations
• Factors and factoring of quadratic polynomials with integer coefficients
• Completing the square in quadratic expressions
• Quadratic formula and factoring of general quadratic polynomials
• Using the quadratic formula to solve equations
Functions
• Linear functions
• Quadratic functions – word problems involving quadratic functions
• Graphs of quadratic functions and completing the square
• Polynomial functions (including graphs of basic functions)
• Simple nonlinear functions (e.g., square and cube root functions ; absolute
value;
rational functions; step functions)
• Rational exponents, radical expressions, and exponential functions
• Logarithmic functions
• Trigonometric functions
• Fitting simple mathematical models to data
Algebra of Polynomials
• Roots and factorization of polynomials
• Complex numbers and operations
• Fundamental theorem of algebra
• Binomial coefficients (and Pascal’s triangle)
• Mathematical induction and the binomial theorem
Combinatorics and Finite Probability
• Combinations and permutations as applications of the binomial theorem and
Pascal’s
Triangle
The preceding list of topics comprises the most basic
elements of school algebra.
The total amount of time spent on covering these topics would normally
be a little more than two years , although how the instruction of these topics
is structured throughout high school is a matter to be determined by each
curriculum. What is usually called “Algebra I” would in most cases, cover
the topics in the Symbols and Expressions, Linear Equations, and at least the
first two bullets of Quadratic Equations. The usual course called “Algebra
II” would cover the rest, although in some cases, the last bullet of Functions
(data), the last two bullets of Algebra of Polynomials (binomial coefficients
and binomial theorem), and Combinatorics and Finite Probability would be
left out. In that case, the latter collection of topics would generally find
their
way into a course on pre-calculus.
The teaching of algebra, like the teaching of all of school mathematics, must
ensure that students are proficient in computational procedures, can reason
precisely, and can formulate and solve problems. For this reason, the preceding
list of topics should not be regarded a collection of disjointed items neatly
packaged to be committed to memory. On the contrary, the teaching should
emphasize the connections as well as the logical progression among the topics.
The following narrative, written with readers in mind who are already familiar
with the curriculum of school algebra, tries to give a brief idea of these
connections
and the main lines of reasoning underlying them. Because standard
texts often treat certain topics incorrectly in the sense of mathematics, a
great
deal of effort has been spent on detailing what these misconceptions are and
how to rectify them.
Symbols and Expressions
It can be argued that the most basic aspect of the learning of algebra is the
fluent use
of symbols. In this context, the concept of a variable occupies a prominent
position. In
standard algebra texts as well as the mathematics education literature, one
rarely finds
an explicit definition of what a “variable” is. The absence of a precise
definition creates a
situation whereby students are asked to understand something which is left
largely unexplained,
and learning difficulties ensue. Sometimes, a variable is described as a
quantity
that changes or varies. The mathematical meaning of the last statement is vague
and
obscure. At other times it is asserted that students’ understanding of this
concept should
be beyond recognizing that letters can be used to stand for unknown numbers in
equations,
but nothing is said about what it is that students should know “beyond” this
recognition.
In [NRC2001], for example, one finds a statement that students emerging from
elementary school often carry the “perception of letters as representing
unknowns but not
variables” (p. 270). The difference between “unknowns” and “variables” is
unfortunately
not clarified. All this adds to the mystery of what a “variable” really is.
In mathematics, a variable is an informal abbreviation for “an element in the
domain
of definition of a function”, which is of course a perfectly well-defined
concept. If, for
example, a function is defined on a set of ordered pairs of numbers, it is
referred to as “a
function of two variables”, and it must be said that, in that case, the emphasis
is more on
the word “two” than on the word “variables”. To the extent that school algebra
intends
to use the concept of a “variable” beyond this narrow context, and in fact
before the
concept of a function is introduced, we proceed to describe a possible
definition of this
concept, one that is at least mathematically correct. In the process, we discuss
the basic
etiquette in the use of symbols, which is after all our main goal.
Let a letter x stand for a number, in the same way that the pronoun “he” stands
for
a man. Any expression in x is then a number, and all the knowledge accumulated
about
rational numbers can now be brought to bear on such expressions. In a situation
where we
have to determine which number x satisfies an equation such as 2x2+x−6 = 0, the
value
of the number x would be unknown for the moment and x is then called an
unknown.
In broad outline, this is all there is to it as far as the use of symbols is
concerned.
A closer examination of this usage reveals some subtleties, however. Consider
first the
following three cases of the equality mn = nm:
(1) mn = nm.
(2) mn = nm for all whole numbers m and n so that 0 ≤ m, n ≤ 10.
(3) mn = nm for all real numbers m and n.
The statement (1) has no meaning, because we don’t know what the symbols m and n
stand for. To give an analogy, suppose someone makes the statement, “He is 7
foot 6.”
Without indicating who “he” refers to, this statement is neither true nor
false. It is
simply meaningless. If m and n in (1) are real numbers,
then (1) is true, but there are
other mathematical objects m and n for which (1) is false. On the other hand,
(2) is
true, but it is a trivial statement because its truth can be checked by
successively letting
both m and n be the numbers 0, 1, 2, . . . , 9, 10, and then computing mn and nm
for
comparison . The statement (3) is however both true and more profound. As
mentioned
implicitly above, this is the commutative law of multiplication among real
numbers. It is
either something you take on faith, or, in some contexts, a not-so-trivial
theorem to prove.
Thus, despite the fact that all three statements (1)–(3) contain the equality mn
= nm,
they are in fact radically different statements because the specifications for
the symbols
m and n are different. Therefore a basic rule concerning the use of symbols is
that
the specifications for the symbols are every bit as important as the symbolic
expressions
themselves.
Next, consider the solution of the linear equation 3x+7 = 5. The usual procedure
for
solving such equations yields 3x = 5 − 7, and therefore
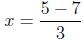
There is a reason why we do not write the solution as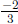
, because we can also consider
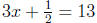and get
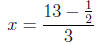
Or consider 3x + 25 = 4.6 and get
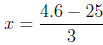
Or consider 5x + 25 = 4.6 and get
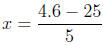
And so on. There is an unmistakable pattern here: no matter what the numbers a,
b, and
c may be, the solution of the linear equation ax + b = c, with a, b, c (a ≠ 0)
understood
to be three fixed numbers throughout this discussion, is
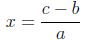
We have now witnessed the fact that in some symbolic expressions, the symbols
stand
for elements in an infinite set of numbers, e.g., the statement that mn = nm
for all
real numbers m and n, while in others, the symbols stand
for fixed values throughout
the discussion, e.g, the numbers a, b, and c in the linear equation ax + b = c.
In the
former case, the symbols are called variables, and in the latter case,
constants. The
main message is, therefore, that
| Prev | Next |