pre algebra distributive property prentice hall,multiplying and dividing powers cheat,simplifying exponents and square root calculator,simplify square root of difference of two squares
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: convert decimal to square root fraction.We have an extensive database of resources on convert decimal to square root fraction. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter! 

---

100	=	1
101	=	10
102	=	100
103	=	1,000
104	=	10,000
105	=	100,000
106	=	1,000,000
etc.

Note: 10ⁿ is equal to 1 followed by n zeros.

When we write a number such as 27,483, the digit 2 stands not for 2, but for 2(10⁴) = 20,000. The digit 7 represents 7(10³) = 7000, etc. The value we associate with each digit comes from its place in the number. The right most digit of a whole number is in the "ones place", the second digit from the right is the "tens place", etc. To extend the decimal system to fractions, we use the reciprocal powers of 10 and the decimal point to separate the "ones place" from the "tenths place".

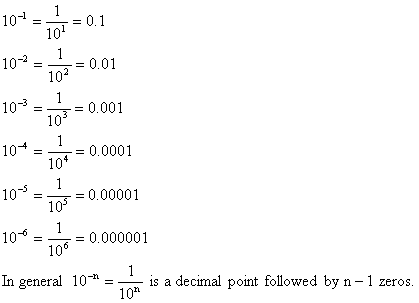
The leading 0 to right of the decimal point is not required for a number smaller than 1. It is used to emphasize the location of the decimal point. A decimal fraction such as 0.375 is interpreted as

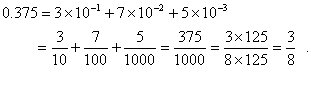
Note: adding extra zeros to the right of the rightmost digit to the right of the decimal point does not change the value of the decimal fraction. It does, however, imply a greater knowledge of the precision of the value.

A decimal fraction like 0.375 is called a terminating decimal because the digits to the right of the decimal point come to an end. The procedure outlined above shows how to convert a terminating decimal to a fraction. It is summarized below:

1. Carry along the digits to the left of the decimal point as the whole number part of the resulting mixed number. If there are no non-zero digits to the left of the decimal point, the decimal represents a proper fraction.

2. Put the digits to the right of the decimal point over the power of 10 that goes with the right most decimal place. For example, in converting 0.1145, 1145 is put over 10,000 since the right most digit, 5, is in the ten-thousandths place.

   

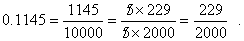
3. Reduce this fraction to lowest terms.

To convert a fraction to a decimal is quite easy. We just translate the fraction bar into a division. Remember that in a mixed number there is an understood but unstated plus sign. So that

This can also be done directly using the Casio fx-300W or TI-30Xa as was discussed in Unit 2.

If a fraction is in lowest terms and its denominator has a factor besides 2 or 5, then that fraction, when converted to a decimal, will generate a repeating decimal. For example, 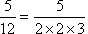, so 12 has a factor of 3 and 5¸12 = 0.41666... = .

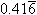The 6s as indicated either by the ellipsis "" or 6 with a bar on top repeat "forever".

Note: all of these ways of writing the repeating decimal are the same. Calculators will display 0.416666667 since they work with a fixed number of digits and will round the last digit displayed.

To convert a repeating decimal into a fraction is a little complicated and is rarely encountered in practical problems. As a result no problems requiring such a conversion occur in the unit exercises. However, if you are curious, the procedure is summarized and illustrated below:

1. Count and record the number of decimal places from the decimal point to the repeating string of digits.

2. Move the decimal point to the left by this number of places.The result is a decimal number where the repeating pattern of digits begins inthe tenths place immediately to the right of the decimal point.

3. The digits to the left of the decimal point of the result from Step 2 become the whole number part of a mixed number. If there are no non-zero digits to the left of the decimal point, then the original decimal began the repeating pattern with the first digit and the whole number part of the mixed number is zero.

4. Add the whole number from Step 3 to a fraction with the repeating digits as the numerator and a string of 9s as the denominator. The number of 9s in the string is equal to the number of repeating digits in the numerator.

5. Take the fraction from Step 4 and divide it by 10 raised to the power of the number from Step 1. This number, worked out as a fraction, is the fraction equivalent to the original repeating decimal.

To illustrate the steps convert 0666...to a fraction.

1. The number of places from the decimal point to the repeating string of 6s is two.
2. The result is the decimal 0.666...
3. The whole number is 0.
4. There is one repeating digit, a 6, so the result is
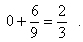
5. Dividing two thirds by 10² = 100 gives
   

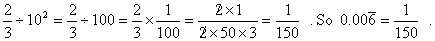
As a more complicated example consider converting 3.1527272727 to a fraction.

1. The number of places from the decimal point to the repeating string of 27s is two.
2. The result is the decimal 315.272727...
3. The whole number is 315.
4. There are two repeating digits, 27, so the result is
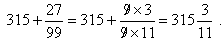
5. Dividing the answer of Step 4 by 10² = 100 gives
   
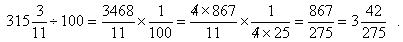
6. Using a calculator we can verify that
   

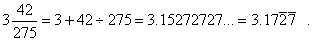
Often we wish to approximate a decimal number by finding another decimal roughly equal to the first number, but expressed with less digits. This process is called rounding. To round use the following procedure:

1. Determine the decimal place to which the number is to be rounded. Often this is stated in the problem or application.

2. If the digit to the right of this decimal place is less than 5, then replace all digits to the right of this decimal place by zeros or discard them if they are to the right of the decimal point.

3. If the digit to the right of the decimal place is 5 or greater, then increase the digit in this decimal place by 1 and replace all digits to the right of this decimal place by zeros or discard them if they are to the right of the decimal point.

As an example, consider rounding 10,547.395 to the different decimal places shownin the following table.

10,547.395 rounded to	Decimal Place of Rounding	Result
2 places	hundredth's place	10,547.40
1 place	tenth's place	10,547.4
the nearest unit	one's place	10,547
the nearest ten	ten's place	10,550
the nearest hundred	hundred's place	10,500
the nearest thousand	thousand's place	11,000

Raising numbers to powers or exponents occurs in many applications. Recall from Unit 1 that bⁿ means a product of n factors of b. The number b is called the base, and n is the power or exponent. So,

1.5745	=	1.574×1.574×1.574×1.574×1.574
	=	9.661034658

This result is correct to as many places as the Casio fx-300W or TI-30Xa display. To perform this calculation on the Casio fx-300W use the keystrokes 1.574 5, while on the TI-30Xa enter 1.574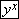5.

Exponents of two and three are very common and have special names; b² is called "b squared" and b³ is called "b cubed". Both the Casio fx-300W and the TI-30Xa have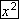 keys to square a number. On the Casio fx-300W it is found in the second row, fourth column, while on the TI-30Xa it is in the third row, third column. When evaluating an expression, the standard order of operations requires that bases be raised to powers before any multiplications or divisions are performed. This hierarchy is built into scientific calculators.

For example, consider evaluating

3.54 × 7.21³ - (10.7 × 6.28)² ¸ 3.56

On the Casio fx-300W this is done with the following keystrokes:

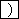
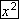
3.54 7.21 3 10.7 6.28 3.56 .
The display shows the answer as 58.46760266. The keystrokes on the TI-30Xa areidentical except that the key is used instead of the key. The Casio fx-300W does have an key in the first row, fifth column, and this key could have been used instead of 3 above.

Consider evaluating 25¹². Entering 25 12 on the Casio fx-300W gives the display 5.960464477¹⁶. Entering 25 12 on the TI-30Xa results in 5.960464478¹⁶.

Because of the large size of the number both calculators have expressed the result in scientific notation. In scientific notation we express the answer as a decimal number between 1 and 10 times ten to a power. Here the number between 1 and 10 is 5.960464478 and the power of 10 is 16. In ordinary decimal notation, which the calculator cant display for lack of space, this answer would be written as 59,604,644,780,000,000. If you try to work with these large decimal numbers, the advantages of scientific notation soon become obvious!

Note: both calculators seem to suggest that the exponent applies to 5.960464478. This is not true. The exponent is on ten, but to save space in the display the calculator does not show the 10.

Now consider (0.04)¹². Both the Casio fx-300W and the TI-30Xa display 1.6777216^-17. The result is in scientific notation with a negative exponent on 10. In ordinary decimal notation this result would be 00000000000000016777216. The left-most non-zero digit, 1, is 16 (17-1) decimal places to the right of the decimal point. Thus, in scientific notation a positive exponent on 10 gives the number of decimal places the decimal point must move to the right to get the ordinary decimal answer, while a negative exponent on 10 gives the number of decimal places the decimal point must move to the left to get the ordinary decimal answer.

To enter a number in scientific notation on the Casio fx-300W, use the key found in the bottom row, third column. For example, to enter 6.02 × 10²³, use the following keystrokes: 6.02 23. A very small number like 7.15 × 10^-12 is entered with7.15 12. Here is the "change sign" or minus key found in the third row, first column.

The procedure used on the TI-30Xa is identical except that the key is used instead of the key and the change sign key is . The key is in the fourth row, second column and the change sign key is in the bottom row,fourth column.

Consider a table of squares of the whole numbers.

N	N2
0	0
1	1
2	4
3	9
4	16
5	25
6	36
7	49
8	64
9	81
10	100
11	121
12	144

If we reverse this table, i.e., start with N² andget the value of N, the table would look like.

N2	N
0	0
1	1
2	1.14121356
3	1.732050808
4	2
5	2.236067977
6	2.449489743
7	2.645751311
8	2.828427125
9	3
10	3.16227766
11	3.31662479
12	3.464101615

The second number is called the square root of the first. In symbols

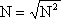
For example:

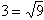
Remember from Unit 1 that the square root symbol acts as a grouping symbol. Any operations inside the square root need to be completed before the root is taken. For example,

.

To perform this computation on the calculator, parentheses need to be inserted around the expression inside the square root symbol. On the Casio fx-300W enter

116 16 ,

while on the TI-30Xa the corresponding keystrokes are:

116 16

A similar table of the cubes of whole numbers can be formed.

N	N3
0	0
1	1
2	8
3	27
4	64
5	125

If we reverse this table, i.e., start with N³ andget the value of N, the table would look like below.

N2	N
0	0
1	1
2	1.25992105
3	1.44224957
4	1.587401052
5	1.709975947
6	1.817120593
7	1.912931183
8	2

The second number is called the cube root of the first. In symbols

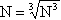
For example:

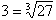
On the Casio fx-300W, the cube root key is in the first row, fourth column. On the TI-30Xa enter 0.

The cube root, like the square root, acts as a groupingsymbol. Any operations inside the cube root need to be completed before theroot is taken. For example,

To perform this computation on the calculator, parentheses need to be inserted around the expression inside the cube root symbol. On the Casio fx-300W enter

85 2 45 ,

while on the TI-30Xa the corresponding keystrokes are:

85 2 45 0

When we are using numbers to express the change in a quantity,such as the amount of money in a checking account or a running backs totalyards, we soon find that the quantities under study dont always increase. Bankaccounts sometimes decline and running backs can lose yards! To represent achange, which decreases, we use negative numbers, while positive numbersrepresent an increase. A convenient way to visualize positive and negativenumbers is the number line shown below. Here the positive (or "ordinary")numbers are to the right of zero and the negative numbers are to the left ofzero.

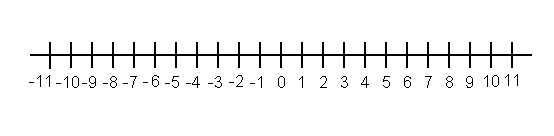
The opposite of 5 is -5 since -5 + 5 = 0. For example, if you lose $5 then make $5, youre back to zero. By the same argument the opposite of -5 is 5. If a running back gains 10 yards, then loses 7, his net yardage is 3. In symbols, 10 + (-7) = 3. So adding a negative 7 is the same as subtracting a positive 7. Also 10 + (-7) = (-7) + 10 = 3. In general, a + ( -b ) = a - b, i.e., subtracting is the same as adding the opposite and visa versa.

Suppose a running back loses 3 yards every time he carried the ball. If he had four carries, his net yardage is -3 + (-3) + (-3) + (-3) = -12 . [You may have noticed that we dont write + -3 , but rather + (-3), this is just to avoid the potential confusion of two adjacent operation symbols.] However, using the definition of whole number multiplication as repeated addition, we see that 4(-3) = -3 + (-3) + (-3) + (-3) = -12. So a positive number times a negative number should result in a negative number. What about a negative times a negative? One of the fundamental rules of arithmetic is called the distributive property. It says that

a×(b + c)	=	a×b + a×c
For example,
5×(4 + 7)	=	5×4 + 5×7 = 20 + 35 = 55
5×11	=	55

Now,

(-1)×(1 + (-1))	=	(-1)×1 + (-1)×(-1)
(-1)×(0)	=	-1 + (-1)×(-1)
0	=	-1 + (-1)×(-1)

So (-1)(-1) added to -1 gives zero. But only 1 added to -1 makes zero. So we conclude that

(-1)(-1) = 1

In general, a negative number times a negative number gives a positive number. We have analogous statements in English. If I say "I am not dishonest", the double negative makes the sentence equivalent to saying "I am honest".

We now have another way of forming the opposite of any number, simply multiply by -1, i.e., -b = (-1)b. The standard order of operations requires that we square before multiplication. This means that -5² = -1(5²) = -25, while (-5)² = (-5)(-5) = 25. Consider now subtracting a negative number as in 10 - (-8) = 10 + (-1)( -8) = 10 + 8 = 18. So subtracting a negative is the same as adding the positive.

Finally, division is the opposite operation to multiplication. Since(-5)(6) = -30, then

(-30)÷(-5)	=	6
(-30)÷6	=	-5
30÷(-5)	=	-6
30÷(-6)	=	-5

In general, a negative number divided by a negative number is a positive number, while a negative divided by a positive or a positive divided by a negative is negative.

To enter a negative number on the Casio fx-300W use the minus sign key before the number just as it is written. For example, to evaluate

enter the following keystrokes:

6 10 3 2

The keystrokes for the TI-30Xa are shown below. Note: you enter the negative numbers "backwards", i.e., first enter the value, then thechange sign key.

6 10 3 2

Exercises:

Perform the indicated operations giving answers to the stated number of decimal places:

Write the following as decimals:

12. = __________

13. = __________

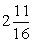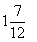Write the following decimals as fractions in lowest terms:

14. 0.45 = __________

15. 8.84 = __________

Calculate the following:

16. -56÷8 = __________

17. (-8)²÷(-16) = __________

18. -8²÷(-16) = __________

19. = __________

20. = __________

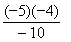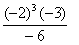Solve the following problems:

21. A stack of eighteen pieces of lumber is 31.50 inches thick. How thick would a stack of thirty-three such sheets be?

    thickness = __________

     

22. A delivery truck gets 11.3 miles per gallon of gasoline. If gas costs $1.12 per gallon, what will be the cost of the gasoline needed to drive 189 miles?(Round to the nearest penny.)

    cost = __________

     

23. A machinist earns $12.50 an hour plus time and a half for overtime (hours worked beyond 40). What is the machinists gross pay for a 53.75 hour work week? (Round to the nearest penny.)

    pay = __________

     

24. In the first six months of the year, Precision Auto Body had the following profit and loss record:
    

    January	$8,736.52	profit
    February	$12,567.34	profit
    March	$1,282.72	loss
    April	$39.998.68	profit
    May	$179.66	loss
    June	$1,257.23	profit

    
    Find the total profit or loss for this six month period.

    profit/loss = __________

     

25. A welder earned $468.75 (gross pay before deductions) for 37.5 hours of work. Find her hourly rate of pay.

    rate = __________

     

26. A cubic foot holds 7.481 gallons. A car has a gas tank which holds 14.5 gallons. To three decimal places, how many cubic feet is this?

    cubic feet = __________

     

Answers:

 

---

Vocational Math I (804-379) Textbook by Al Lehnen, Madison Area Technical College
| |

 

	© 2002 by Al Lehnen; HTML-ized ( or ).
	This document was Wednesday, August 21, 2002, 4:10 PM.