pre algebra distributive property prentice hall,multiplying and dividing powers cheat,convert decimal to square root fraction,simplifying exponents and square root calculator
Thank you for visiting our site! You landed on this page because you entered a search term similar to this: simplify square root of difference of two squares, here's the result:

---

Irrational numbers are real numbers that cannot be expressed as the ratio of two integers.

Common irrational numbers are nonrepeating and nonterminating decimals.These include the roots of any prime and most radicals.

Pythagoras's Proof that the is irrational

Given below is Pythagoras's proof of the existence of irrational numbers using the as an example.

Simplifying Radicals

The symbol , is called a radical. The number underneath the symbol is the radicand. n is the root index, indicatingwhat the root is. When no number appears, 2 meaning square root is assumed.

canalso be written as 2^½. In general, x^a/b means the bth root of x^a.Such rational exponents still follow the rules given inlesson 4.

Statements	Reasons
= a/b	Proof by contradiction: assume true what we are proving false
2=a2/b2   2b2=a2	Square both sides (expressions remain equal)
a and b have no common factors	assumed without loss of generality: a/b represents reduced fraction
If a is odd, a2 is odd, but 2b2 is clearly even, a contradiction	odd times odd is odd, a cannot be both even and odd simultaneously.
If a is even, let a=2c	even can be factored into 2 and another number even (2) times anything is even
a2 = a·a = 4c2 = 2b2	Substitution of equals into product (twice)
2c2= b2	Division Property of Equality
So b is even; hence a,b have the common factor 2, a contradiction.	Q.E.D.   (quod erat demonstrandum:     Latin for which was to be proved.)

When simplifying radicals, break the radicand into factors of perfect squares, cubes, etc. ( 9is the perfect square of 3, 4 is the perfect square of 2, 27 is the cube of 3). Separate the factors into separate radicals. Then express the roots of the radicals with perfect squares, cubes...For example:

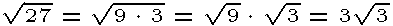
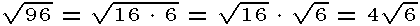
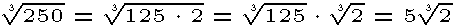
Multiplying Radicals

When multiplying radicals, multiply the radicands of like root indexes and then simplify the product. Usually, the easiest way is to simplify as you go along so that you don't end up with large products to factor. Examples: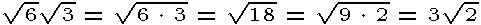

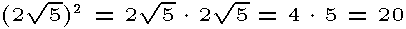
Compare the next two examples and notice how they differ. Both methods are correct. Choose the one which saves you the most time.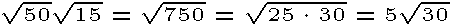

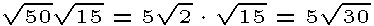
Note when the radicals have different root indexes: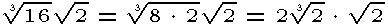

Rationalizing Denominators

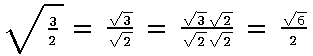
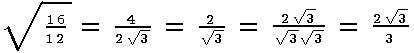
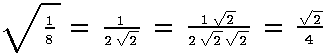
Common practice is to simplify expressions to get rid of radicals in the denominator of fractions. Historically, this was all but necessary before calculators.(Imagine dividing by the by long division!)In order to rationalize the demoninator, the common practice of multiplying by one is used. One comes in many forms: anything divided by itself is one. So multiply the fractionby the square root that is in the denominator over itself.For example:

Extracting Roots

The can be approximated on your calculator. Before calculators were developed, the following methodwas widely taught and used. It is based on Newton's Method which will be taught in calculus.Since the decimal representation of goes on forever without terminating or repeating,calculators can only give you a fairly precise decimal approximation.

Whenever you use the decimal approximation of a radical, you should note that it is an approximation and not exact by the use of the symbol.

1. Separate the number into groups of two digits going each way from the decimal point.
2. Estimate the largest square which will go into the first group.
3. This number goes both in the normal divisor's location for long division and above the first group as in long division.
4. Double this digit and bring it down for the next step (see example below).
5. Also bring down the next group of digits as in long division.
6. Estimate how many times the two digit number formed using this doubled digit and the number of times...will go into the number.
7. Repeat steps 4-6 above, but now the number down will be 2, 3, 4 digits,etc. Continue until the desired accuracy is achieved.

Example of extracting root 2.

Step 1:

		?.??????______________
?	/	2. 00 00 00 00 00 00

Find an integer that squared goes into 2:

		1_______________
1	/	2. 00 00 00 00 00 00