Thank you for visiting our site! You landed on this page because you entered a search term similar to this: multiplying and dividing powers cheat, here's the result:
Rational Expressions
The quotient of two polynomials is called a rational expression. Rational expressions are to . The goal here is to learn to do everything that you do with Rational Numbers with rational expressions. The isn't too difficult as long as you know two things well, rational number arithmetic and polynomial factoring. If you need some review on either of these please read Rational Numbers or Factoring Polynomials. It is also a good idea to have an understanding of finding LCMs of numbers by prime factoring, because we will be doing the same thing for polynomials. For review on that see How to Prime Factor a Number and GCFs and LCMs.
Simplification
Simplification is also called reducing to lowest terms with number fractions. When you reduce fractions to lowest terms you divide top and bottom by common factors. See Rational Numbers for an explanation of why this can be done. With algebraic fractions you do the same thing, and you must remember that it is only common factors that you can divide out. You normally keep track of what you are doing with this by factoring the top and bottom and then crossing out any factors that are the same upstairs as downstairs, but make sure you remember that you are taking out common factors, so you must factor before you cancel anything out, and you can only cross out common factors of the whole top and bottom, not just anything that looks the same upstairs and downstairs. In general in algebra if you are ever unsure about whether you can do something one way you can test it out is to replace the variables with numbers and see if what you are thinking about doing would still make sense.Example 1:
Simplify.Solution:
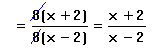
Explanation:
Before doing any simplifying we must factor in the style that we factor polynomials. If these were numbers you'd actually do the addition and subtraction before trying to take out a common factor, but you can't do that here, because you don't know what x is. So the only way you can hope to take out a common factor is to factor by the methods that you use to factor polynomials. In this case we are in luck, because both the top and the bottom have common factors. And then when we factor them that way, we do in fact get a common factor in the top and bottom that we can divide out. So we divide top and bottom by 8 and we can show this in a kind of shorthand notation by crossing out the two 8's. This kind of canceling notation is a very useful shorthand, but you must be very careful not to misuse it. No, we can't go any farther in this problem. Don't be tempted to cancel out the x's, they are not factors. Neither x+2 nor x-2 will factor, so there can be no more common factors to take out.Example 2:
Simplify.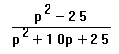
Solution:
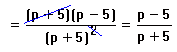
Explanation:
Same thing here except that the factoring is a bit more complication. Here the top is a difference of squares and the bottom is a perfect square. I've written the canceling in a funny sort of way that isn't really quite legal, but it works here. I am canceling the p+5 upstairs with one of the p+5's downstairs, and as a quick way of showing it I just crossing out the 2. Be careful if you do this. It will only work if the exponent is 2. Otherwise you have to lower the exponent by one. Again this is as far as we can go. The p's in the final expression won't cancel, because they are not common factors. Neither p-5 nor p+5 will factor.Multiplication
To multiply rational expressions, multiply straight across, the numerator by the numerator and the denominator by the denominator. See Rational Numbers for an explanation of why. You should also be sure to do cross canceling to keep from having to simplify at the end. Factor everything in sight and then cancel out any factor that is upstairs with any factor that is downstairs, no matter where they are in the problem.Example 3:
Multiply.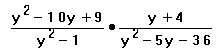
Solution:
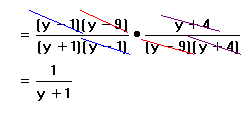
Explanation:
Factor everything in sight and then start canceling. For the first top we are looking for two numbers to multiply to 9 and add to 10, so that is 1 and 9, but it is really -1 and -9 because the middle term is negative. For the second bottom we are looking for two numbers to multiply to 36 and subtract to 5. That would be 9 and 4. Since the middle term is negative we want the bigger one, the 9 to be negative and the smaller one, the 4 to be positive. See Factoring Polynomials for an explanation of this kind of thinking when factoring polynomials. Lots of things cancel out here. I have color coded it so that you can see what cancels with what. After canceling we multiply everything that is left. If nothing is left there is always a 1.Example 4:
Multiply.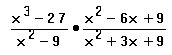
Solution:
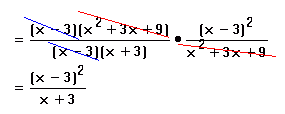
Explanation:
Here we need the difference of cubes formula to factor. It doesn't matter that the denominator of the second one won't factor, because it is going to cancel out anyway. As to the form of the final answer, in my class and probably in many other algebra classes it is considered to be all right to leave your answer in factored form, because it is just a lot of extra work doing something that you already have been tested on to multiply everything out, and really factored form is just as good a form for a polynomial as standard form.Division
To divide, just like with numbers, you invert the second one and multiply. See Rational Numbers for an explanation why. To multiply, see the instructions above.Example 5:
Divide.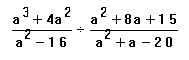
Solution:
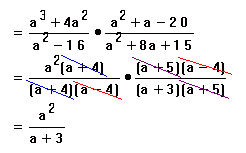
Explanation:
Turn the second one upside down right away and after that everything goes the same as with multiplication. Lots of factoring practice in one like this.LCMs
For adding and subtracting rational expressions we need to be able to find LCMs of polynomials. To do this we can use the same prime factoring method that we use with numbers. See GCFs and LCMs. The idea is that the factorization of each of the polynomials has to occur in the factorization of the LCM so that it will be a multiple, but we don't want to use any more factors than necessary, so that it will be the LEAST common multiple. Keep in mind if you get confused with this that your answer must be a multiple of each of the given polynomials.One thing that is different with polynomials is that when we are dealing with numbers we don't normally use negative numbers, so it is not possible for something to be only off by a minus sign from something else. This is possible with polynomials, and it is good to know what to do about it. What you do basically is that you ignore it. Signs of the whole polynomial don't matter for LCMs, because you can always multiply one by -1 to get the other.
Example 6:
Find the LCM.Solution:
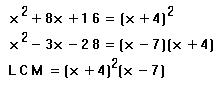
Explanation:
We can use here the same prime factoring technique that we use with numbers, except that here prime factoring is the kind of factoring that we do with polynomials. (See GCFs and LCMs for an explanation of the prime factoring technique for numbers.) We factor the polynomials and put together the factors in the smallest way possible so that each of the factorizations are contained in it. This means that we include all of the factors to the highest powers that they occur in a single polynomial. The first polynomial here is a perfect square. For the second polynomial we are looking for two numbers that multiply to 28 and subtract to 3. (See Factoring Polynomials.) Then we see that there are two prime factors, x+4, and x-7. The highest power of x+4 is 2 and the highest power of x-7 is 1.Example 7:
Find the LCM.Solution:
Explanation:
Here the y-1 and the 1-y factors are only off by a factor of -1, which doesn't matter for LCMs. We can tell that they are off by a factor of -1, because they are reverse subtractions. Subtraction isn't commutative. The order makes a difference with it, but it makes a difference in a very specific predictable way. Try some numbers to see it for yourself. If you subtract 7-5 you get 2, but if you subtract 5-7 you get -2. Since factors of -1 don't matter for LCMs whenever you want, you can reverse a subtraction. Remember, though, that this doesn't mean that y-1 and 1-y are the same. They are just different in a way that doesn't matter for finding LCMs. And it doesn't matter in the answer either. If you gave the answer as 10(1-y), that would be okay too. It would still by a multiple of the two polynomials, and no more complicated.Addition and Subtraction
If the denominators are the same, just add or subtract the numerators. But unlike with multiplication you may still have to simplify after this. If one denominator is off by a factor of -1 from the other, you can fix that pretty easily, you just multiply one of them top and bottom by -1. When the denominators are totally different is when it get a bit trickier. Just like with numbers, you have to find a common denominator. The common denominator is the LCM, but you can't just change the denominators to the LCM for free, because that would change the value of the expressions. You have to look and see what is missing in the denominators and multiply top and bottom by that. See Rational Numbers for an explanation of why we have to do it this way.Example 8:
Add.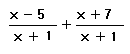
Solution:
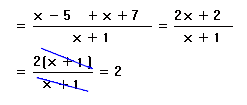
Explanation:
Here the denominators are the same, so we just add the numerators. But unlike with multiplication there is no way to avoid having to simplify at the end, but again you can't just cancel the x's, you have to first take the 2 out as common factor. In the end we could have a 1 in the denominator, but 1's in the denominator aren't necessary.Example 9:
Add.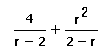
Solution:
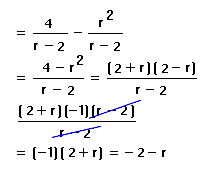
Explanation:
Here the denominators are almost the same, but the differences are backward. Even though I said that this doesn't make a difference for LCMs, there is something that needs to be done in this case when we are adding, namely we need to make the denominators the same by multiplying one of the fractions top and bottom by -1. It doesn't really make a difference which one. It might have even been better if I had used the other one. In this problem I multiplied the second fraction top and bottom by -1 and that made it subtraction instead of addition. Then the problem had another minus sign twist to it, which is that when I factored in order to try to simplify it, it turned out that it almost, but not quite had a common factor. Again we were off by a factor of -1 which I factored out so that I could cancel. You don't really have to do this quite so elaborately as this. If I were doing it on my own I which just cancel the two differences that were reversed and replace the top one with a minus sign or a -1. Also if you are in my class it is okay to leave it as -1(2+r) or -(2+r), but it is better to at least use the second of these and perhaps better to multiply it out, since that is a pretty simple multiplication.Example 10:
Add.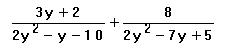
Solution:
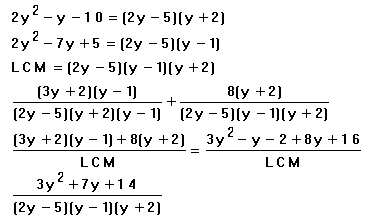
Explanation:
Now here we have one with totally different denominators, so we have to find a proper LCM. We factor the two polynomials (see Factoring Polynomials for a review of how to do this kind of factoring) and see that they have a common factor, which we don't have to include twice in our LCM. Since there are no powers, we just include all of the factors that are there, without any repetition, so we get the product of the three factors for our LCM. To see how to express each of these fractions as fraction with the LCM as the denominator what we have to do is look and see which factors are missing. In the first fraction the y-1 is missing, so we multiply it top and bottom by that. In the second fraction the y+2 is missing, so we multiply top and bottom by that, and then we get something much uglier, but still it is something we can deal with because we have common denominators. Once the denominators are the same, just like before, we just add the numerators.I tend to find it to be advisable in problems like this there are complicated to write in some kind of substitute for the denominator, because there is a lot to do with the numerator and copying the denominator over and over again can get a bit tedious. I've written LCM here, but D for denominator would do as well. This also has the advantage that it keeps you from trying to cancel things out too soon in incorrect ways. Because of the very nature of these problems with multiplying top and bottom by things in order to get common denominators, it will always look like there is a common factor to take out before you do the simplifying in the numerator, but this is not the case, because you can only cancel common factors of the whole numerator. There is no short way around it, you have to multiply each bit out and then combine like terms, and then try to factor that before you can look for anything to cancel.
After we get the numerator totally simplified, then we can put the denominator back in. Then we can try to factor the numerator and see if it has any common factors with the denominator. One thing that is interesting here is that you can cheat a bit when you are factoring it, because you don't really care if it factors, if it doesn't factor so that one of the factors is the same as one of the ones in the denominator. So here we can write (3y )(y ) as the form of the factorization and only consider possibilities where there is a -1 or a 2 in the second factors, since there is no way for the first factor to match up. It can't be a -1, since the terms are all positive, so the only possibility would be the 2, which would have to be a factorization of (3y+7)(y+2), but that gives a middle term of 13y, so it doesn't work. Since this is the only possible factorization that could cancel with anything, we don't really care if it factors any other way, so we leave it unfactored.
Example 11:
Perform the indicated operations.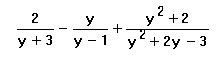
Solution:
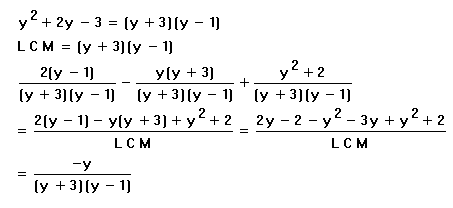
Explanation:
Here we have three fractions to deal with, so we need to find the LCM of all of them. This is not too bad since the third one is the product of the other two, so it is the LCM. What is missing in the first fraction is y-1, so we multiply that top and bottom. What is missing in the second fraction is y+3, so we multiply that top and bottom. The third one already has the common denominator, so we don't have to change it. Then we do the adding and subtracting in the numerator and do all of the multiplying and combining like terms before putting the denominator back in. The numerator simplified quite a lot, so it is easy to see that there is nothing in it to cancel with the denominator and we are done.More Examples and Practice
To see some more examples, including some with more than one variable, and get more practice see my MathHelp problem set collection Rational Expressions.