Thank you for visiting our site! You landed on this page because you entered a search term similar to this: free on line calculator to convert lineal metres to square metres.We have an extensive database of resources on free on line calculator to convert lineal metres to square metres. Below is one of them. If you need further help, please take a look at our software "Algebrator", a software program that can solve any algebra problem you enter!
| |
(Please read the Disclaimer)

Contents for Part 2: Geographical Information Systems

This unit presents Geographical Information Systems, an indispensabletool for map analysis and presentation for land evaluation. Tworelated topics are presented in this unit, because of their importancefor geographic analysis: Digital Elevation Models and the GlobalPositioning System.

1 GIS : Introduction and orientation
Almost always a land evaluation presents its results as maps.In addition, the location and other spatial characteristicsof evaluation units are often important land characteristicsin the evaluation itself. In this set of lectures we studyGIS and remote sensing as applied to land evaluation only.There are many other uses of GIS, e.g., facilities managementand network analysis, that we will not study.
1.1 GIS General References
(Burrough, 1986) is the best text on GIS for land evaluation;(Tomlin, 1990) presents a coherent and rational method of spatialanalysis with many examples in land use planning. An encyclopedicoverview of GIS and its applications is (Maguire, Goodchild &Rhind, 1991). Most GIS programs come with tutorials; the serieswith IDRISI (Eastman, 1992) and Arc/INFO (Environmental SystemsResearch Institute, 1993) are both good. The IDRISI project, undercontract from UNITAR, has produced a series of workbooks withsample datasets for change and time-series analysis (Eastman &McKendry, 1991), forestry applications (McKendry et al.,1992), coastal-zone management, and decision making under uncertainty(Eastman et al., 1993).
1.2 Sources of information on GIS and digital datasets
The is indispensable for definitions, addressesof data sources etc. This list is posted to the comp.infosystems.gisand news.answers news groups on a monthly basis; from there youcan save it to a file and print it The most current version isavailable via anonymous FTP on 'abraxas.adelphi.edu' in the file'/pub/gis/FAQ'
Digital Chart of the World
The Digital Chart of the World is a 1.7 GB digital geographicdatabase that is available on CD-ROM. It was input from 1:1,000,000Operational Navigation Charts and 1:2,000,000 Joint NavigationCharts of the Defense Mapping Agency. It includes 17 layers, aeronauticalinformation, data quality info, drainage, supplemental drainage,hypsography, hypsography supplemental, land cover, ocean features,physiography, political/ocean, populated places, railroads, transportationstructure, utilities, and vegetation. Note the coarse scale ofthe source maps. Also some areas of the world are much more reliablethan others. Mann Library reference has a copy of this data set
Global Resource Information Center (GRID)
This is a system of cooperating centers, organized by the UnitedNations Environmental Program, that is dedicated to making environmentalinformation more accessible to analysts and decision makers. Theycollect digital data from a wide variety of sources, and makeit available free or for the cost of reproduction.
There is on-line access by ftp to 'grid2.cr.usgs.gov', or underWWW at . There are six offices worldwide; the most accessible fromthe USA is at the EROS Data Center in South Dakota, e-mail ''.
1.3 Definition
A GIS is an assemblage of computer equipment and a setof computer programs for the:
- entry and editing,
- Storage,
- query and retrieval,
- Transformation,
- analysis, and
- display (soft copy) and printing (hard copy)
... of spatial data.
Key point: All data in a GIS is georeferenced, i.e.located by means of geographical coordinates with respect to somereference system. This is how a GIS differs from computer-aideddrafting or graphics program.
1.4 Components of a GIS
Hardware: processor (CPU), often a mathematical co-processor,temporary memory, graphic display and video memory, on-line storage(magnetic or optical disk), off-line storage (tape, removabledisks), input devices (keyboard, pointing device, digitizing tablet,scanner), output devices (line plotter, color graphics printer).From quite inexpensive ($1,000) to very expensive ($100,000).May have a network of computers sharing their peripherals.
Operating system (OS): controls the hardware (and networkif any) and executes programs. High-performance GISs almost allwork under the UNIX OS or another minicomputer/workstation OS(e.g., VMS). Microcomputer OSs: Microsoft MS-DOS, IBM PC-DOS,Macintosh. Multitasking and network-ready microcomputer OSs: IBMOS/2, Microsoft Windows NT.
Software: modules for map and legend data entry and editing,data transformation (e.g. map projections), data management, dataretrieval (queries), map display and output, map analysis. From'free' (public domain) to inexpensive (<$1,000) to quite expensive($100,000) for specialized analysis.
As with all other areas of computation, GIS technology is constantlybecoming more powerful and less expensive. The trend is towardsmore power to the individual user on the one hand, and bettercoordination between users on the others (e.g. shared data bases).

2 Coordinate systems & map projections
Since all data in a GIS must be georeferenced, the question naturallyarises, referenced to what? Answer: a coordinate system.
A simple explanation of projections, coordinates and datums isin (Eastman, 1993) p 22-27, a bit more complicated in (AmericanSociety of Photogrammetry, 1980) p. 413-421. A standard referenceis (Snyder, 1987). Strahler's various physical geography textsalso have simple explanations.
2.1 Spherical coordinates
Two coordinates determine the position on the surface of earth'sellipsoid: Latitude (north or south of the equator) andlongitude (east or west of the standard meridian at Greenwich,England the last remnant of England's imperial 'glory' to theInternational Date Line at 180°E/W in the middle of the PacificOcean)
Latitude and longitude are measured in (arc)degrees (360°in a circle), (arc)minutes (60' in 1°) and (arc)seconds(60" in 1"). The mean minute of latitude defines onenautical mile = 1,852m. Therefore the equator-to-pole distanceis (1/60' ° x 90°) x 1/1.852km' = 10,000 km exactly.An arc-second of latitude, and of longitude at the equator, isthus 1,852/60 = 30.866m. A degree of latitude, and of longitudeat the equator, is 60° 1/1.852km ° = 111.12km.
All Lat/Long references must be referred to a standard datum,which consists of a reference ellipsoid and coordinateorigin. A datum specifies a coordinate system and the positionsof known control points in that system. The origin is at (0°,0°) as defined by the prime meridian (Greenwich) and theequator. Lat/Long references with different datums may be substantiallydifferent (100s of meters between ground points with the samecoordinates) between the various ellipsoids.
Advantage: one system for the entire earth, more-or-lessconforms to the shape of the earth, so no systematic distortions.
Disadvantage: spherical not planimetric, must use sphericaltrigonometry to measure areas and distances, must project ontoflat maps where the grid lines are curved.
2.2 Planimetric coordinates & the UTM projection
Points on the ellipsoid are projected to a flat piece ofpaper (a 2-dimensional map). Many projections, varying in theirproperties: can't have all of: (1) equal areas, (2) truedirections, and (3) a single scale over the wholemap. The most common projection in international land evaluationapplications at medium to large scales is the Universal Transmercatoror UTM projection (American Society of Photogrammetry,1980) p. 419-420, (Davis et al., 1981) p. 571-576. At continentalscales, the Albers Equal-area projection is often used.
The UTM projection was intended for military purposes over relativelysmall areas. In the Mercator projection a straight line has constantcompass bearing.
Distortion is controlled by orienting the projection to a north-southcentral meridians (so the projection is Transversalwith respect to the equator), and by dividing the earth in 60strips (zones), each covering 6° of longitude (approx.667.8km wide at the equator). The scale is exact on two meridiansper strip and has a maximum error of 1 part in 1000 at the edgesof the strip; the error is 1 in 2500 along the central meridian.Zone 1 is from 180°E/W (the International Date Line) eastto 174°W, and so eastward to Zone 60 from 174°E to 180°E/W.There is an overlap of 30' between adjacent zones.
The equator is assigned 0m in the northern hemisphere, 10,000,000min the southern, so that Y (north-south) coordinates are alwayspositive.
The central meridian is assigned the coordinate 500,000m, so thatwith the zone being at most 667km wide, there are no negativecoordinates in X (east-west) either.
Even though areas and distances are not exactly represented onthe map, it is more than precise enough for land evaluation andregistering remotely-sensed information at project and even regionalscales.
2.3 Conversion between projections
All projections are based on exact mathematical formulas, so canbe inter-converted. But the datum and reference ellipsoid mustbe specified. (IDRISI module PROJECT, projections are describedin DESCREF, listed in LISTREF, edited with EDIT Option 7.)
2.4 Elevations
Elevations are measured in meters above or below mean sea level,a known vertical coordinate defined by the geodetic survey ofthe country. This is the same whether the X & Y coordinatesare spherical or planimetric. In the case of spherical coordinates,the elevations are on the radius of the sphere; for planimetriccoordinates, they are in the vertical dimension, orthogonal tothe two horizontal coordinates X & Y.

3 Digital map representations: grid & vector
The key question is, how do we represent the features of a map(by extension, features on or near the surface of the earth) inthe computer? The computer contains a digital representationof the map, which it can manipulate and present. There are twoconceptual representations used in GISs: grid (sometimescalled 'raster') and vector. These are very different waysof thinking about geography, which lead to very different methodsof analysis.
3.1 The grid or 'raster' representation of a map
Basic idea: the map area is divided into cells (sometimeserroneously called pixels, see below), normally squareor at least rectangular, on a regular grid. Each cell issupposedly homogeneous, in that the map is incapable of providinginformation at any resolution finer than the individual cell.The map shows exactly one value (land use, elevation, politicaldivision...) for each cell.
(Formerly, this representation was referred to as a raster.The name 'raster' comes from the original display technology:a scanning CRT, like a television screen, and refers to the left-to-right,top-to-bottom scanning.)
Key point: The grid cell is the only unit of spatialinformation and analysis.
Different themes are stored as separate maps (also calledoverlays or coverages), which are related by a commoncoordinate system. For example, there may be one map of populationcenters, another of political subdivisions, another of geology,another of land cover, etc., all covering the same area.
This is a very simple representation in the computer: conceptually,a 2-D matrix of values which correspond to a grid placed overthe paper map.
| 3 | 3 | 3 | 6 | 6 | 6 | 6 | 6 |
| 3 | 3 | 6 | 6 | 6 | 2 | 2 | 2 |
| 3 | 3 | 3 | 6 | 6 | 6 | 2 | 2 |
| 5 | 3 | 5 | 4 | 6 | 4 | 2 | 1 |
| 5 | 5 | 4 | 4 | 4 | 4 | 1 | 3 |
The resolution of the map is the lineal dimension of thecell times 2 (diagonal). Note there is no scale of a gridmap, only a resolution.
Graphic representation: on the computer screen or printerwith one or more pixels ('picture elements') which arethe smallest areas of the display device that can receive a separategraphic treatment (color or intensity).
The graphic scale depends on the actual size of the imageon the output device compared with the feature being represented.
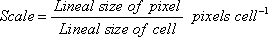
For example, a printed page of 216mm width, divided into 80 printerpositions, gives 2.7mm/pixel. Suppose 2 cells must be representedby each pixel (contraction by a factor of two), gives 0.5 pixels/cell. Suppose each cell represents 30m x 30m on the ground,i.e., the lineal size of the cell is 30,000mm. Graphic scale:(2.7/30,000) x 0.5 = 00045 = 1:22,222.
3.2 Advantages of the grid representation
- Simple concept
- Easy management within the computer; many computer languagesdeal effectively with matrices (including special-purpose matrixlanguages like MATLAB and APL).
- Map overlay and algebra is simple: cell-by-cell
- Native format for satellite imagery
- Suitable for scanned images
- Modeling and interpolation is simple, because the grid ofdata is dense and complete
- Cheap technology
3.3 Disadvantages of the grid representation
- Fixed resolution, can't be improved. So when combiningmaps of various resolutions, must accept the coarsest resolution
- Information loss at any resolution, increasingly expensivestorage and processing requirements to increase resolution
- Large amount of data especially at high resolution
- Not appropriate for high-quality cartography (line drawing)
- Slow transformations of projections (must transform each cell)
- Some kinds of map analysis (e.g. networks) is difficult orat least not 'natural'.
Note: there are more advanced data types based on a variable-sizegrid (finer where more detail is needed) that do away disadvantages(1), (2), and (3), but the advantages (2), (3) and (6) becomeless applicable. Commercial system based on 'quadtrees': SPANS.
3.4 The vector representation of a map
Basic idea: points on a map are stored in the computerwith their 'exact' (to the precision of the original map and thestorage capacity of the computer) coordinates.
-- Points can be connected to form lines (straight or describedby some other parametric function) or chains;
-- Chains can be connected back to the starting point to enclosepolygons or areas.
Each of these spatial entities may have an identifierwhich is a key to an attached database containingthe attributes (tabular data) about the entity. All theinformation about a set of spatial entities can be kept together,i.e., multi-thematic maps.
Example: a point which represents a population center may havea database entry for its name, population, mean income etc. Aline which represents a road may have a database entry for itsroute number, number of lanes, traffic capacity etc. A polygonwhich represents a soil map unit may have a database entry forthe various soil characteristics (depth, parent material, fieldtexture...).
(The name 'vector' comes from the connection between points bymeans of a line with specified magnitude and direction,and from the original display technology: CRT with controllableelectron beam.)
3.5 Topology
In the vector representation, the various geographic entities(points, chains, polygons) have a definite spatial relation calledtopology. Although as humans we perceive these spatialrelations without even thinking about them, they must be explicitfor the computer. Some examples:
(1) Connectedness: lines are connected at nodes.
(2) Adjacency: polygons are adjacent if they share a commonboundary line.
(3) Containment: one polygon can contain another as an'island'.
Topology can be stored as part of the map representation (in thedatabase tables) or built as needed from the coordinates of eachentity.
In the grid representation, the only topology is cell adjacency,and this is implicit in the representation (i.e., definedby the grid addresses), not explicit as in vector topology.
3.6 Advantages of the vector representation
- Precision is only limited by the quality of the original data(very rarely by the computer representation);
- Very space-efficient, since only points about which thereis information or which form parts of boundaries are stored, informationfor the areas between such points are inferred from the topology;
- Explicit topology makes some kinds of spatial analysis easy;
- High-quality output.
3.7 Disadvantages of the vector representation
- Not suitable for continuous surfaces such as scanned or remotely-sensedimages and models based on these;
- More expensive hardware and (especially) software.
3.8 Converting from vector to grid
A common operation is converting vectors (points, linesor polygons) to a grid map; this processes is often referredto as rasterizing a vector map. The basic idea is simple:(1) set up a grid, (2) scan the vectors, placing the vector identifierin each grid cell where it occurs (points or lines) or which isbounded by the vector (polygons). In IDRISI, these steps are accomplishedwith modules INITIAL (step 1) and POINTRAS, LINERAS or POLYRAS,depending on the type of entity to be converted (step 2).
A major question is: To what grid resolution should a vectormap be converted? This depends on the scale of the papermap from which the vector map was created. The basic idea is toretain the minimum legible delineation (MLD), which isa concept that depends on map scale (Forbes, Rossiter & VanWambeke, 1982), in the grid map. The MLD is conventionally definedas 0.4cm² to 0.25cm² on the map; we will use the higher-resolutiondefinition, i.e., 0.25cm², which represents a square of 0.5cmon each side.
Step 1: Determine the scale factor of the originalmap. Example: 1:1'000,000 has a scale factor of 1'0000 or 10E+6.The units of the scale factor are (ground distance)÷(map distance),e.g. (ground cm)÷(map cm).
Step 2: Convert the 0.5cm side of the MLD square to mapscale, by multiplying by the scale factor. This tells us how muchground distance is represented by the side of the MLD. Example:(0.5×1/10² m) × (1/106 m m) = 5×10³ m = 5km.
Step 3: To preserve cartographic accuracy, divide the grounddistance by 2. This ensures a more pleasing grid map without excessiveand false precision or excessive storage requirement. Example:5km÷2 = 2.5km = 2,500m. This is the lineal resolutionto be used when creating the grid image, e.g., using IDIRISI's'INITIAL' command.

4 Data types and basic operations on maps
For a thorough treatment see (Burrough, 1986) Chapter 5.
4.1 Data types
It is crucial to know, for each map, the type of data itrepresents. Although the computer may represent all data typesby numbers, this is only for convenience; conceptually the datatype is derived from the kind of information being represented.Operations must be consistent with data types or the resultwill be meaningless.
(Example: what is the meaning of (political subdivision code)/ (soil textural class)??)
1. 'Continuous' values are represented by integeror floating-point (computer approximation to real) numbers (e.g.,elevation, reflectance, vegetation index). Two kinds of scales:
1a. A ratio scale has a natural zero, so ratiosof two numbers on this scale have meaning. Example: population.It makes sense to say 'New York City has 1,000 times the populationof Ithaca'.
1b. The interval (also called ordinal)scale has no natural zero. The origin ('zero') of the scale isassigned for convenience, therefore ratios have no meaning. Example:temperature in °C. It makes no sense to say 'today's maximumtemperature of 30°C is twice yesterday's of 15°c'; althoughmathematically this is true it has no meaning.
Note: the only difference between continuous integers and continuousfloating-point is the fineness of the measurement scale, neitheris truly 'continuous' mathematically.
2. Classes, with a natural order , are representedby integer codes(e.g., increasingly-steep slope classes); theseare called ordinal classes.
3. Classes, no natural order, are represented byinteger codes (e.g., political subdivisions or land cover classes,here alphabetic order might be considered 'natural' but reallyit is just an accident). Also called a nominal classes.
4. Logical, Boolean, 0/1, true/false, yes/no, included/excludedare usually represented by the numerical values 0 and 1. But theycan't be added etc. in the same sense as the integers 0 and 1,their arithmetic follows Boolean logic.
5. Continuous classification values (sometimes called'fuzzy' values) are real numbers on the interval [0,1], whichrepresent varying degrees of membership in the class. These area generalization of Boolean or logical values.
4.2 Commensurate variables
A set of variables are said to be commensurate if theyhave the same scale of measurement. This is independent of whetherthey have the same data type.
Example: hydraulic conductivity can be measured in any units of(1/length time); these are not commensurate unless a conversionfactor is applied.
Example: a continuous variable 'soil depth' measured in cm, anda classified variable 'soil depth classes', each class definedby a range of depth also measured in cm, are commensurate.
4.3 Updating a map
Non-zero areas of the first map overwrite any values of the second.So the non-zero points, lines or areas contain corrected values.Example of new points: new climate stations. Example of new lines:new roads. Example of new areas: new suburban subdivisions.
IDRISI command OVERLAY option 7
4.4 Querying a map
Given the map, we will want to extract information from it.
4.4.1 What is the value at a point?
IDRISI command COLOR (display), subcommand 'x' or 'c', shows thecoordinates and value. In the case of classified maps, shows theclass (legend category).
4.4.2 What is the value over a region?
Uses two maps: the map containing the values (the image)and the map which defines the region(s) for which the values shouldbe determined (the geographic definition). The geographicdefinition is used to divide up the image, and the values correspondingto each geographic entity are aggregated in various ways: minimum,maximum, sum, mean, range, standard deviation.
Example: if each cell of the image contains a vegetation index,and the geographic definitions are forestry management units,EXTRACT/average would produce a map of the average vegetationdensity of each forest unit.
Caution! the operation must make sense given the data type. Forexample, averages only makes sense with continuous values. Noneof these make sense with unordered classes.
IDRISI command EXTRACT
4.5 Transforming one map
4.5.1 Grouping or transforming classes
Class-to-class function. E.g. from a map of 12 soil textural classes(sand, sandy loam, loamy sand, ..., silty clay loam, clay loam,clay) to one of three general classes ('coarse', 'medium', 'fine').Can never increase the number of classes (information content).This is sometimes referred to as re-classifying a map,because the existing classification is being replaced with a newclassification.
IDRISI command ASSIGN (RECLASS can also be used here).
4.5.2 Classifying continuous values
Continuous-to-class function. Used to group a continuous variable,e.g. slope % to slope classes.
IDRISI command RECLASS.
4.5.3 Transforming continuous values
Logarithm, exponential, power, reciprocal... any univariate functionof the data values, which must be continuous.
IDRISI commands SCALAR, TRANSFORM.
4.5.4 Identifying individual polygons
Finds and numbers individual polygons (connected areaswith the same value).
IDRISI command GROUP.
4.6 Working with more than one map
To work with more than one map at a time, the coverages must:
(1) be registered to the same coordinate system;
(2) cover the same land area;
(3) in a grid representation, have the same resolutionand origin.
The following sections outline the procedures to ensure that points(1) (3) are satisfied.
4.6.1 Register to the same coordinate system
Some maps (already georeferenced) may have to be transformedto another projection. Basic procedure:
- establish the mathematical relation between points in thetwo projections
- create a blank map in the new projection at the desired resolution
- fill in the cells by projecting values from the original map
Problem: cells in new image (projected) rarely correspond to cellsin the original image.
IDRISI command: PROJECT
4.6.2 Cover the same land area
Use a windowing operation to make a sub-image of the larger image;we can only analyze the area for which we have complete coverage.
IDRISI commands: WINDOW, SUBSET
4.6.3 Make the resolutions identical (grid images)
If the two images do not have the same cell size, one orboth must be adjusted, because grid overlays are cell-by-cell.
Simple case: the cell sizes are even multiples.
E.g., Land cover classification from SPOT panchromatic imageryat 10mx10m resolution, to be compared with a land cover classificationfrom Landsat TM image at 30mx30m resolution. One Landsat TM cellcovers exactly the same area as 3x3 = 9 SPOT cells.
We have two possible solutions: increase the apparent resolutionof the coarser image or decrease the actual resolution of thefiner image.
Solution 1: expand the image with the coarser (larger)cell size by an even multiple. The value in the original cellwill be entered in each of the new, smaller cells covering itsoriginal area.
IDRISI command: EXPAND
Major problem with Solution 1: the expanded image promises moreinformation than it actually has. It was not sampled at the resolutionat which it is presented. Still, this may be justifiable if itis known that the theme is quite homogeneous across large areas(low-frequency features), so that the only errors are at the bordersbetween themes, which may appear wider than they really are andare not accurate to within the apparent resolution of the newmap. Example: map of political units.
Solution 2: contract the image with the finer (smaller)cell size by an even multiple. We are losing informationin the contracted image, but at least we are not misrepresentingthe sampling density, as in Solution 1. The value in one new cellmust somehow represent the values in several original cells. Severalpossibilities:
IDRISI command: CONTRACT
(1) Pixel thinning: simply use the value in the upper-leftmost(or, any arbitrarily-chosen) original cell of the window to becontracted. This corresponds to coarser sampling. This is thebest choice for maps of nominal classes. Example: land cover classes.
(2) Pixel aggregation: some function of the original setof values is used to obtain the new value. This has several possibilities:
(2.1) Average: appropriate for continuous variables, such as reflectances(remote-sensing images)
(2.2) Maximum or minimum value: appropriate for ordinal classes.The analyst chooses to minimize or maximize according to the purpose.
(2.3) Mode: most usual value. A good choice for nominal classeswhen 9 or more cells are being aggregated, not enough samplesto be feasible for smaller windows.
Harder case: the cell sizes are not even multiples.
E.g., a Digital Elevation Model is available with 90m horizontalresolution, and a soils map has been prepared with 50m resolution.
Solution 1: if one of the maps was prepared from a vectormap, re-rasterize to the resolution of the othermap., always supposing that the new resolution is justified bythe scale of the original map.
IDIRISI commands: POLYRAS, LINERAS, POINTRAS, following INITIAL
Solution 2: Resample one of the maps to the other'sresolution. Basic procedure:
IDRISI command: RESAMPLE
(1) Set up an output map on the grid of the map that won't beresampled (the project standard)
(2) Fill in the cells of the new grid with values from the originalmap. How to fill?
(2.1) Center value: use value from the original map at the centerof the new grid.
(2.2) Aggregate the values from the original map that areincluded in the new cell. Possibilities: weighted average(by area of the cell to be filled): only appropriate for mapsof continuous values; most likely value (like a mode),picking the one single value that covers the most area of thecell to be filled. Can aggregate only in the new cell or basedon a window.
4.7 Combining two or more maps
4.7.1 Arithmetically combining continuous values
Purpose: derive a map from a set of source maps, all of whichrepresent continuous values, based on some multivariate function.
Add, subtract, multiply, divide, normalized ratio. In general.any multivariate function, with the 'variables' being the mapvalues.
IDRISI command: OVERLAY, options 16. Division only makes sensewith ratio-scale data. None make sense with classed values.
4.7.2 Combining Boolean values
Purpose: combine a set of source maps, all of which representBoolean values, based on some truth function.
AND, OR etc.: binary logical operators. Common use: to combinepartial suitability maps into final suitability. Examples: 'Areasthat are zoned for the use AND are physically suited to it'. 'Areasthat are suitable for cotton OR for maize but are NOT suitablefor housing developments'.
IDRISI command: OVERLAY, multiply or minimum (for AND) or maximum(for OR). Works on '0/1 maps', 0 = false, 1 = true.
4.7.3 Choosing the minimum or maximum value
Purpose: determine the extreme value, for commensurate continuousvariables or ordinal classes.
IDRISI command: OVERLAY, options 8 & 9. OK for ordinal classes(e.g., maximum suitability class).
4.7.4 Identifying which map has the maximum value
Typical use: identifying the 'best' use: the source maps representthe predicted 'value' of each land use, and must be measured onthe same scale.
IDRISI command: MDCHOICE.
4.7.5 Cross-tabulating
Purpose: Identify all combinations of two classified maps (maximumnumber of result classes n x m, in practice most maps havesome correlation so that not all classes actually occur). Example:soil groups x climate zones = soil-climate homogeneous regions.
This is a very common operation for defining 'homogeneous' mapunits for land evaluation.
IDRISI command: CROSSTAB.
4.7.6 Cutting out areas
Purpose: Limit the area of one map to a defined area on a secondmap. Also called 'masking'. Example: map 1 = soils of NY state,map 2 = Tompkins County (as 0/1 map), result map = soils of TompkinsCounty (blanks outside the county boundary).
IDRISI command: OVERLAY, multiply, the mask image must containonly 0's (in the area to be eliminated) and 1's (in the areasto be retained).
4.8 Analyzing single maps
Map analysis does not alter a map or create new maps, instead,it extracts facts about existing maps.
4.8.1 Descriptive statistics
For continuous variables, a histogram and descriptive statistics.Can be used to identify breakpoints for classification. For classifiedvariables, a frequency distribution of classes.
IDRISI command: HISTO.
4.8.2 Area, perimeter
Almost always we want to know how much land is in each suitabilityclass. The perimeter is less commonly measured but can be usefulfor estimating how much fence is needed etc. Good-bye planimeter!
IDRISI commands: AREA, PERIM, compactness ratio CRATIO
4.8.3 Spatial autocorrelation
How similar are nearby cells? (later lecture on spatial variability)Only makes sense for continuous variables.
IDRISI command: AUTOCORR, correlates adjacent cells. For larger'lags', CONTRACT the map first.
4.9 Analyzing two maps together
4.9.1 Correlation and regression
To what degree can one map be used to predict the values on another?and what is the mathematical expression of that relation? Example:temperature vs. elevation in the tropics.
For continuous variables, linear regression etc. (IDRISI command:REGRESS)
For classified variables, chi-square & related statisticsbased on cross-tabulation (IDRISI commands: CONFUSE, CROSSTAB)

5 Spatial analysis of geographically-based land characteristics
In this lecture we talk about geographically-based land characteristicsimportant for land evaluation and how they can be determined thespatial analysis in a GIS.
There are some land characteristics that have a geographic expressionand can be mapped with a GIS but which do not require spatialanalysis. Example: current land use, political entity, land tenure.
5.1 Distance
The distance of a land area to a feature (point, line or area)is important for many uses. Examples: by law a certain use maybe prohibited within 1km of a national park; irrigation by smallpumps may only be practical within 100m of a permanent stream.These are examples of buffer zones.
For polygonal map units, the distances of its interior pointsmust be aggregated in some way. Possibilities: minimum distance(closest point), maximum distance (furthest point), average distance,distance to the centroid ('center of gravity' of the polygon).
IDRISI command: DISTANCE
5.2 Transportation cost
A more general form of 'distance'. The 'cost' (difficulty) ofmoving from one point to another is determined both by distanceand by the 'resistance' of the path between the points. More expensive(in terms of time, money or both) to travel on a paved highwayvs. a dirt road, to walk over a mountain than across a plain,to walk through dense vegetation than sparse etc.
Two maps: target (as in distance) and cost surface: eachcell has a relative cost (1.0 = standard).
IDRISI command COST.
5.3 Allocation to 'nearest' feature
Assign each cell of the map to its 'nearest' of a set of targetfeatures (e.g., school, market, well). Distance can be true distanceor a cost. Then the land characteristic is the identifier of the'nearest' feature.
IDRISI command ALLOCATE, follow-on to DISTANCE or COST
5.4 Land area
A land use may require a certain minimum (or, less commonly,maximum) contiguous area. For example, forest plantationsless than 20ha may not be worth the effort to build an accessroad. The GIS can compute the area of each polygon of a suitabilitymap, and discard those that are too small.
IDRISI command: GROUP the polygons of the suitability map, calculatetheir AREA, RECLASS those that are too small to 'unsuited - toosmall' and those that are large enough to 0 (background), COVERthe original suitability map with the 0/1 map of too-small areas.
5.5 Adjacency
Some land uses may be prohibited adjacent to other uses(e.g. no agriculture adjacent to a national park).
Some land uses may require adjacency, e.g., a rule thatsuburban development must be located adjacent to existing urbanor suburban areas. Or a LUT may require two kinds of land together:e.g., dairy farms with both pasture and grain.
This is different from a buffer zone, because in the present casewe visualize the planning units as already being specified.
In a vector system with polygon topology, a query such as 'showall polygons adjacent to polygons with land use A' are trivial.In a grid system this is more difficult; IDRISI provides no primitivecommand to do this.

6 Digital Elevation Models (DEM) for land evaluation
(Burrough, 1986) Chapter 3
The digital elevation model, abbreviation 'DEM', is an extremelyuseful product of a GIS for land evaluation. Basic question: howdo we represent the three-dimensional structure of the earth'ssurface in the computer, and what can we infer from this representation?
Definition of a DEM: "digital representation of the continuousvariation of relief over space". 'Relief'can be any continuous variable that depends on geographic coordinates.The most common is elevation above mean sea level. The exact samerepresentations and techniques can be applied to continuoussoil characteristics (pH, depth, ...), climate characteristics(rainfall, evaporation,...), vegetation characteristics (biomass,greenness...).
Note: some people reserve the term 'DEM' for what we call 'gridDEM', 'altitude matrix', or 'gridded DEM'. Then the more generalterm is 'Digital Terrain Model' (DTM).
There is no ideal DEM, because the full complexity of a surfacecan not be captured by the computer; there is always a samplingproblem and a representation problem. Various samplingschemes and representations may lead to very different resultsboth in the DEM itself and especially in its derivatives. Cautionis advised in this highly-technical specialty that is still somewhatof a black art). The accuracy of the individual elevationsdoes not necessary ensure the accuracy of derivatives such asslope maps.
There are two general ways to represent a surface: by a mathematicalfunction that expresses elevation as a function of the horizontalcoordinates, and by an image of the surface, explicitlygiving the elevation at some set of points, with no functionaldependence with horizontal coordinates.
6.1 Representing a surface: mathematical methods
Basic idea: Fit a continuous three-dimensional functionto sample points ('elevations'), and then the elevation at anypoint can be determined by evaluating the function at that point.
Advantages: very compact representation, smooths noisydata from observational and sampling errors.
Disadvantages: smooths abrupt changes and extreme pointseven if they are real. The smoother the surface to be represented,the more appropriate this method.
6.1.1 Global trend surfaces
One function for the entire map.
Polynomials of various orders with the geographic coordinatesas independent variables (higher-order polynomials allow interactionsbetween the coordinates). Fourier series for periodic surfaces(dunes).
Common in geology (e.g. elevation or thickness of a formation)
Example: ![]()
Here the elevation 'z' is a 2nd-degree (quadratic) polynomialfunction of the two coordinates 'x' and 'y' with a reference levelbo and an interaction term with parameter b4.
The polynomial is fitted by least-squares estimation.
IDRISI command: TREND.
6.1.2 Local patches
Piecewise functions, each applicable over some area of the map,must have equal values at the edge of the patches although thederivatives may not be continuous. Various orders of continuityare possible with thin-plate splines (Wahba, 1990).
Regular or irregular patches.
Not visually pleasing, not common in cartography.
Commonly used in Computer-Aided Design (CAD).
6.2 Representing a surface: image methods
6.2.1 Regular grid or altitude matrix: grid DEM
The surface is represented by a matrix of elevations on a regulargrid. Exactly a grid data structure.
Problems are as with any grid structure: tradeoff of resolutionand storage requirement; over and under-sampling (matching gridto terrain complexity)
Advantages: simple data structure, simple data entry. Widely usedfor hydrologic modeling, e.g. (Abbott et al., )
6.2.2 Irregular grid: Triangulated Irregular Network (TIN)
The surface is represented as a sheet of edge-connected of triangularfacets based on Delaunay triangulation of irregularly-spaced controlpoints. Advantages: can explicitly follow stream and ridge lines;sampling can be intensified in areas of high slope complexityand made sparse in other areas. Some computations (e.g., slope)are very efficient.
6.2.3 Lines
The surface is represented by isolines ('contours'). This is themethod used on most topographic maps.
Rarely used for digital models, except for data entry (see below).
6.3 Sampling strategies for a DEM
Basic question: what sort of sampling strategy do we use to createDEM? and what processing will the computer have to do on the samples?The sampling may be well-matched with a particular representationmethod or not.
6.3.1 Regularly-spaced point observations
Record the elevation at regular-spaced grid points. Field surveyor by overlaying the grid on a topographic map.
Advantage: already a grid DEM with no further processing.Suitable for trend surfaces.
Disadvantage: inefficient sampling, although progressivesampling on increasingly-finer grids according to relief complexityis possible (still must store all the redundant points)
Disadvantage: the highest/lowest points on the landscapeare rarely sampled, since they aren't likely to fall directlyon the sample grid.
6.3.2 Irregularly-spaced point observations
Record the elevation at selected points.
Advantage: can include the highest/lowest points; can increasesampling in zones of high relief. Suitable for trend surfaces.
Advantage: can be directly represented as a TIN
Must interpolate to unsampled points for a grid DEM. IDRISI commandINTERPOL. Sophisticated interpolation procedures and terrain-specificsampling schemes give better results, e.g. (Hutchinson, 1989).
6.3.3 Contours (isolines)
Follow the same elevation and draw a line representing it. Typicallyby stereoplotters from stereo pairs of aerial photos.
Advantage: 'infinitely dense' information along the contours,inter-contour spacing is closest in zones of high relief.
Disadvantage: highest/lowest contours are never the highestor lowest points. Can supplement a derived grid or TIN DEM withthese points. Interpolation methods may not give satisfactoryresults if the contour interval is too sparse.
Must interpolate to unsampled points for a grid DEM. IDRISI commandINTERCON.
Must create tie-lines for a TIN.
6.4 Products derived from a DEM, useful in land evaluation
6.4.1 Slope, Aspect, Form
See (Burrough, 1986) p. 49-52, also (Evans, 1980)
Slope is a critical land characteristic for all land usesthat I can think of. It affects land qualities such as runoff,erosion hazard, moisture balance, landslide or slump hazard (catastrophicerosion). Sometimes called gradient. It is defined as themaximum derivative in any direction of a plane tangent to thesurface as modeled by the DEM.
Aspect or orientation is an important land characteristicfor land qualities having to do with insolation and winds. Itis the normal to the plane, projected onto the X-Y plane.
Form (concavity, convexity in various directions) is importantin determining direction and velocity of surface water flow. Theseare defined as the various partial derivatives of the DEM.
Global trend surface: each point has a first total derivative,maximize this to find the normal (aspect) and gradient (slope).
TIN: each triangular facet has a slope (angle of inclination ofthe triangle) and the normal to the facet gives the aspect.
Altitude matrix (grid DEM): the local neighborhood of nine cellsis considered as a small patch of nine sample points; the maximumdifference in Z (corrected for diagonal) is the slope and thedirection of this slope is the aspect. IDRISI command SURFACE.
The slope (gradient) G for the central cell of a 9cell(3x3) neighborhood is:
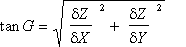
i.e., the sum by quadrature of the gradients in the X and Y directions,where X is the distance across the 9x9 grid and Z is the elevationdifference. There are various ways to estimate these quotientsfrom the actual elevations.
The aspect from a 9-cell neighborhood is:
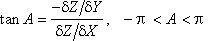
6.4.2 Contour maps (isolines)
The DEM can be used to create maps of isolines (i.e., linesof equal value, in this case, equal elevation) for visualizationor to separate land units on the basis of elevation. There aregood commercial (e.g. SURFER) and public-domain (e.g. GEO-EAS)programs to draw the contours. There is no single 'correct' wayto interpolate contours; see (Davis, 1986) pp. 353-377 for a goodintroduction to the various techniques.
6.4.3 Drainage basin
Given the slope and aspect, and a target drainage system(e.g. its outlet or the main stream), the computer can followthe terrain to the inter-basin divides, and divide the landscapeinto watersheds. (Mark, 1984; Marks, Dozier & Frew, 1984)
These are useful for automatically generating map units in watershedanalysis.
IDRISI command: WATRSHED. Problems with spurious pits (lowpoints with no apparent outlet, usually caused by sampling error)can be avoided by previous FILTER, but then the divides may becomediffuse. The procedure of (Hutchinson, 1989) overcomes these difficulties.
6.4.4 Drainage network
The drainage network can be inferred by following the presumedsurface water flow through the DEM and noting when it is concentratedenough to form an intermittent stream, then a permanent stream,then a river.
6.4.5 Analytical shading
Projective geometry can be used to simulate the illumination ofa landscape from a given point. Often used to created shaded reliefmaps. This is a nice presentation tool. It can also be used todetermine hours of insolation for each site in mountainous terrain:simulate the direct illumination at various intervals and sumthe hours of sunlight.
6.5 Ready-made DEMs
The obvious utility of DEMs has lead to demand from many users,so that some national mapping agencies are creating DEMs for saleor by network access (US Government)
- USA: Based on USGS 7.5" topographic sheets (1:24,000),sampling is 30m horizontal resolution. Vertical sampling was 10'or 20' contours, unclear if the DEM was interpolated from thecontours or from the original stereomodel (this would be moreaccurate).
- World: Digital Chart of the World (DCW): The contourlines can be used to create a DEM. Also there is a ready-madeDEM at a resolution 3" of arc (about 90m N-S and E-W at theequator).

7 Global Positioning System (GPS) for land evaluation
Reference: (Leick, 1990), trade publication 'GPS World'
The Global Positioning System or 'GPS' is a set of satellitescollectively called the NAVSTAR series developed by the US for military navigation. It has revolutionized locationdetermination, especially in remote areas with few identifiablelandmarks, and in areas with poorly-developed survey.
In land evaluation, the principal uses are:
(1) the rapid construction of base maps with acceptableaccuracy; in fact with appropriate techniques it is even possibleto substitute for traditional land survey (Leick, 1990);
(2) the determination of the location of ground-truth sitesfor remote sensing;
(3) the determination of the location of control pointsto rectify existing maps that did not have adequate ground control,so that these may be used in a GIS.
Problems: a very demanding technology fraught with pitfallsfor the unwary, all the way from field work to data reduction.But these are rapidly being simplified for the 'lay' (non-GPSor surveying specialist) user.

8 References
|

Wednesday, October 18, 1995
This page is brought by
Please send us your comments!
Disclaimer: These notes were developed for the CornellUniversity course Soil, Crop & Atmospheric Sciences 494 'SpecialTopics in Soil, Crop & Atmospheric Sciences: Land evaluation,with emphasis on computer applications', Spring Semester 1994,and were subsequently expanded and formatted for publication. They are not to be considered as a definitive text on land evaluation.
Copyright David G. Rossiter 1994. Complete or partialreproduction of these notes is permitted if and only if this noteis included. Sale of these notes or any copy is strictly prohibited.
All contents
This page URL is: