LOWEST COMMON DENOMINATOR LCM CODES

fractions to decimals convertion chart ,   add subtract multiply divide integers worksheet , decimals to radical fractions chart ,   free on line calculator to convert lineal metres to square metres, solving equations by adding subtraction multiply divide
 Thank you for visiting our site! You landed on this page because you entered a search term similar to this: lowest common denominator LCM codes, here's the result: 

---

CS 330

Home

Schedule

Resources

Homework 6
Recursive programming with integers

Estimated time: 3 hours

Acceptance tests for Assignment 6
About acceptance tests

The objective of this homework is to familiarize yourselves with functions and recursive procedures .

Exercises

Additional voluntary exercises

1. Fibonacci (second part). Write a new version of Fibonacci FastFibb, where the number of recursive calls for N is in O(n) . Help: use a function with one (or several) accumulator parameters. What is the invariant of this function?

2. Divisors and multiples. Into arithmetic, one frequentlyuses highest common factor between two whole numbers. Onecan define it as a function gcd with two integer parameters whichsatisfies the properties

   gcd(m, n) = gcd(n, m)
   gcd(m, n) = gcd(m+n, n)
   gcd(m, m) = m

   From the second property, one can derive

   gcd(m, n) = gcd(r, n) , where R is theremainder of the division of m by n.

   Implement a function GCD in OZ, by using these properties. This function takes two whole parameters. Help: Under quelle(s) condition is the derived property useful, i.e. R != m ?

   Implement a function LCM taking two whole parameters and returning their lowest common multiple . Re-use your function GCD.

3. Classification of the points of the plan. There is a relatively simple technique to assign a natural number to each pair of natural numbers (x, y) . The following figure illustratesthe technique, which consists in numbering the successive diagonals of theplanar quadrant. The numbers of the points are in blue.

   

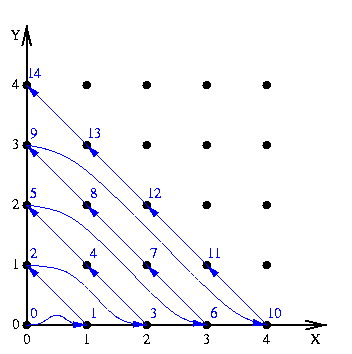
   Write a function Number taking as parameter two naturalnumbers x and y , and returning their number according tothe technique illustrated above. We propose two techniques.

   • Express the number of a point according to the number of its predecessor. The predecessor is defined behind while following the blue arrows. Forexample, the successive predecessors of (3, 2) are (4, 1) , (5, 0) , (0, 4) , (1, 3) ... Implement aniterative version of Number.

   • Improve the effectiveness of your function on the basis of two following observations. First of all, a point (X, y) is on thesame diagonal as the point (x+y, 0) . Then, the number of a pointon the x axis, of the form (X, 0) , corresponds to the number ofpoints in the triangle (0, 0) , (x-1, 0) , (0, x-1) . And this number is a triangular number ...

   • Being given a number N , can you find the co-ordinates (x, y) of the corresponding point? Help: Find initially co-ordinate X by comparing N with the numbers of the points of the type (X, 0) . Then, calculate the co-ordinate y. Are your functions iterative? What is their invariant?

4. Under the paving stones... a pavement philosophizer posesthe following question: `` How many ways can I pave a square surfacewhose sides are of integer length N with identical square paving stones of integer length and cover the whole square? '' the example below shows four possible pavings for n=6 . From left to right, paving stones whose side lengths are 6, 3, 2and 1 were used.

   

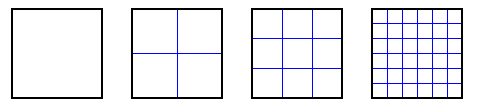
   • Write a function NumberPaves which takes N in parameter and returns the number of pavings in question.
     

   • Suppose now that the paver carries out all possible pavings. How many paving stones will it have used? In the n=6 example , there is 1+4+9+36=50 of it . Write a function NumberPaves who takes N in parameter and returns this number.
     

---