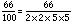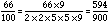Thank you for visiting our site! You landed on this page because you entered a search term similar to this: least common denominator calculator, here's the result:
| x > y | x is greater than y | x > y | x is greater than or equal to y | |
| x < y | x is less than y | x < y | x is less than or equal to y |
When comparing and ordering fractions, we will use this notationinstead of typing out "is greater than," or "isless than." There are two possible scenarios we need to consider.
Case 1: Comparing Fractions
When the denominators are the same
When the denominators are the same, comparing fractions is easy.We simply compare the numerators. This case was discussed in thefirst section of this booklet. If you wish to review that section,
Finding the Least Common Denominator (LCD)
When denominators are different, you must use equivalent fractionsas a tool to create new fractions with the same denominator. Thiswill make them easy to compare. This new denominator is calledthe least common denominator (LCD). The leastcommon denominator is the smallestnumber which is a common multipleof each of the original denominators.
Finding the LCD of a Set of Fractions
|
To elaborate how these steps are done, let's work through thesesteps with two fractions. Let's find the LCD for 10/24 and 22/45:
- Write the prime factorization for the denominator of each fraction.
- Prime factors of 24 are: 2, 2, 2, and 3.
- Prime factors of 45 are: 3, 3 and 5.
- Prime factors of 24 are: 2, 2, 2, and 3.
- Note all prime factors that occur. For each prime factor that occurs, determine in which denominator it occurs the most. Write down the prime factor the number of times it occurs in that one denominator.
- The prime factors that occur are 2, 2, 2, 3, 3, and 5.
NOTE: The prime factor 2 occurred most often in 24, so we write that three times. The prime factor 3 occurred most often in 45, so we write that two times, the 5 occurred only once in 45, so we write that once.
- Calculate the LCD of your fractions. To do this, multiply the factors written down in step 2.
2 x 2 x 2 x 3 x 3 x 5 = 360 The LCD for these two fractions is 360.
Let's look at another example of this.
Example
Find the LCD for the following group of fractions: 9/12, 14/18, 66/100.
The answer to this is 900.
Let's work through the solution to this example.
- Write the prime factorization for the denominator of each fraction.
We must write the prime factors of 12, 18, and 100.
- Prime factors of 12 are: 2, 2, and 3
- Prime factors of 18 are: 2, 3, and 3
- Prime factors of 100 are: 2, 2, 5, and 5
- Note all prime factors that occur.
For each prime factor that occurs, determine in which denominator it occurs the most. Write down the prime factor the number of times it occurs in that one denominator.
In this case, the 2 is a prime factor for all three of the denominators. We must take 2 the number of times it occurs most in any one denominator. It occurs twice. This is also the case for both 3 and 5.
This leaves us with the following prime factors for our LCD:- The prime factors that occur are 2, 2, 3, 3, 5, and 5.
- Calculate the LCD of your fractions. To do this, multiply the factors selected in step 2.
The LCD for our fractions is 2 x 2 x 3 x 3 x 5 x 5 = 900.
Finding the LCD for a group of fractions is an important stepto comparing fractions that have different denominators.
Case 2: Comparing Fractions
When the denominators are different
When we want to compare fractions it is easier to do when theyhave the same denominator. To compare fractions that have differentdenominators we must convert them all to a set of fractions thathave the same denominator, the LCD. There are three steps to comparingfractions when the denominators are different.
Comparing Fractions that have Different Denominators
|
Now let's look back at the example we started working on inthe previous section. Let's determine which is larger: 10/24 or22/45
- Find the LCD for the group of fractions you are comparing.
We found the LCD for these fractions in the last section. The LCD is 360. - Find the multiplier for each fraction. Multiply both the top and bottom of each fraction by that multiplier.
As you should remember from above, to get the LCD we multiplied 2 x 2 x 2 x 3 x 3 x 5 = 360. Look at our fraction with its denominator written out as prime factors.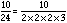 
If we compare the denominator 10/24 to 2 x 2 x 2 x 3 x 3 x 5 = 360, the factors missing are 3 and 5. Since 3 x 5 = 15, the multiplier that is missing is 15. This means we must multiply both the top and bottom of 10/24 by 15.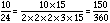 
Now let's do this for the fraction 22/45.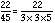 
Here we notice the missing factors are 2, 2, and 2. Since 2 x 2 x 2 = 8, the multiplier that is missing is 8. We must multiply both the top and bottom of this fraction by 8.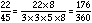 
- Compare and order the numerators of each fraction.
So, we can now see that the fractions we are comparing are 150/360 and 176/360. When we look at these two fractions:
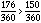which means that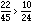 
Now let's look at another example, below.
Example
Order the following fractions from smallest to largest: 9/12,14/18, 66/100.
The answer to this is:
Let's work through the solution to this example.
- Find the LCD for the group of fractions you are comparing.
The LCD for our fractions is 2 x 2 x 3 x 3 x 5 x 5 = 900 - Find the multiplier for each fraction. Multiply both the top and bottom of each fraction by that multiplier.
Starting with 9/12:
If we compare the denominator to 2 x 2 x 3 x 3 x 5 x 5 = 900, we are missing prime factors 3, 5, and 5. Since 3 x 5 x 5= 75, the multiplier for this fraction is 75.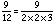
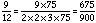
For 14/18:
If we compare the denominator to 2 x 2 x 3 x 3 x 5 x 5 = 900, we are missing prime factors 2, 5, and 5. Since 2 x 5 x 5 = 50, the multiplier for this fraction is 50.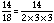
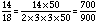
For 66/100:
If we compare the denominator to 2 x 2 x 3 x 3 x 5 x 5 = 900, we are missing prime factors 3, and 3. Since 3 x 3 = 9, the multiplier for this fraction is 9.
