Thank you for visiting our site! You landed on this page because you entered a search term similar to this: solving 2nd order differential equation, here's the result:
33.2 Solving Second Order Differential Equations
We suppose that we have a second order differential equation with dependent variable u and independent variable t. The harmonic oscillator or pendulum are good examples. We suppose, further, that we are given initial values of u and u', as well as a formula for u" in terms of u, u' and t
u" = f(u, u', t)
If f does not involve u or u' we could integrate both sides of the equation once to find u', and again to find u, with a linear function ct + d that must be determined from the initial values.
Thus the problem we face is not unlike that of performing a double integral. However, it is surprisingly easy to do, on a spreadsheet.
We will use an approximation technique that has the order of accuracy of the trapezoid rule; improvements can be obtained by extrapolating as with most numerical methods.
We begin by describing the basic approach.
We will use a column to represent each the variables t, u, u' and u". The first three of these will start at the given initial values of these variables; and the initial value of u" can be computed from them.
In each successive row, t will increase by a constant amount, d. (You can later choose to make d smaller than your initial choice when variables change too much in one d interval.)
We will set
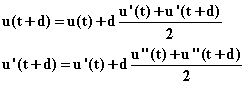
(Which are generic statements, independent of the equation itself.)
Finally we provide an expression for u"(t + d). In doing so we cannot use u(t + d) or u'(t + d) or else our definitions would be circular. On the other hand we would like to use something which averages the second derivative at the ends of the time interval between t and t + d (at least to some order), just as the is done above for u and u'. For the value of u" at t we use f(t, u(t), u'(t)). For the value of u" at t + d we use
u"(t + d) = f(t + d, u(t) + d * u'(t), u'(t) + d * f(t, u(t), u'(t)))
Thus we use the linear approximation to u and u' in f(t + d, u, u') defined at t and evaluated at t + d. We could do slightly better by using a quadratic approximation
![]()
which would be correct to second order, but the trapezoid rule is already in error in second order, so this will not do much good, usually.
You can observe the behavior of u and u' as a function of t by plotting the first three columns (using the "charting" capability of the spreadsheet program with xy scatter plots). You can observe the "phase plane" behavior of the solution by plotting the second and third columns, namely u' vs. u.
If you do things right you can change d or parameters in f in one keystroke, and watch how the solutions change as you change them.
You can handle equations with several dependent variables, like those of planetary motion, by the same approach; with motion in the xy plane you can have a column for t, x, y, x', y', x" and y", and can observe trajectories and look at behavior in the xy plane as you change parameters.
By changing d, and observing how much the solution you obtain changes, you can get a pretty good idea of its accuracy.