second order differential equation solvers

SECOND ORDER DIFFERENTIAL EQUATION SOLVERS

multiplying and dividing fractions and integers worksheet , solving non square non linear system of equation , solving simultaneous linear equations pedagogy, Rewriting Algebraic Expressions with zero and negative exponents

Thank you for visiting our site! You landed on this page because you entered a search term similar to this: second order differential equation solvers, here's the result:

SUNY at Stony Brook MAT 142 Honors Calculus II

Notes on Second Order Differential Equations
Anthony Phillips -- Fall 1998

1. The general second order homogeneous linear differentialequation with constant coefficients looks like

a₂y'' + a₁y' + a₀y =0,

where y is an unknown function of the variable x. If a₂ =0 thisbecomes a first order linear equation which we know how to solve. Sowe will consider the case $a_2 \neq 0$ .Then we can divide through by a₂ and obtain the equivalent equation

y'' + c₁y' + c₀y = 0

with c₁=a₁/a₂ and c₀=a₀/a₂. ``Linear with constant coefficients''means that each term in the equation is a constant times y or aderivative of y. ``Homogeneous'' excludes equations likey'' + c₁y' + c₀y =f(x) which can be solved, in certain importantcases, by an extension of the methods we will study here.

2. The method of solution that we will work on involveslooking for an exponential-type solution

$\begin{displaymath}y=e^{\textstyle \lambda x}.\end{displaymath}$

Why? Because it works! We substitute $y=e^{\lambda x}$ in our equation. Thisgives

$\begin{displaymath}\lambda^2e^{\lambda x}+c_1\lambda e^{\lambda x}+c_0e^{\lambda x}=0.\end{displaymath}$

Since $e^{\lambda x}\neq 0$ we can divide through and get

$\begin{displaymath}\lambda^2 + c_1\lambda + c_0 = 0.\end{displaymath}$

If we solve this quadratic equation for $\lambda$ ,then $y=e^{\lambda x}$ willautomatically be a solution of our differential equation. So thesubstitution $y=e^{\lambda x}$ transforms the differential equation intoan algebraic equation! This equation is called the characteristicequation (associated to the differential equation).

3. The solution of $a\lambda^2 + b\lambda + c = 0$ is(``quadratic formula'')

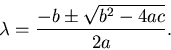
$\begin{displaymath}\lambda = \frac{\textstyle -b\pm\sqrt{b^2-4ac}}{\textstyle 2a}.\end{displaymath}$

In this case a=1, b=c₁, c=c₀, so the solution is

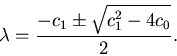
$\begin{displaymath}\lambda = \frac{\textstyle -c_1\pm\sqrt{c_1^2-4c_0}}{\textstyle 2}.\end{displaymath}$

If the discriminant c₁²-4c₀ is positive, then there are twosolutions, one for the plus sign and one for the minus.

Example 1. If the differential equation is y''-y=0 (so c₁=0 and c₀=-1) the roots of the characteristicequation $\lambda^2-1=0$ are $\lambda=\frac{\pm\sqrt{4}}{2} = \pm 1$ .Both y=e^x and y=e^-x are solutions. (Check this!)

Example 2. If the differential equation is y''+y'-2y=0 the roots of the characteristicequation $\lambda^2+\lambda-2=0$ are $\lambda=\frac{-1\pm\sqrt{1+8}}{2} =\frac{-1\pm3}{2}$ ,so $\lambda_1 = 1$ and $\lambda_2 = -2$ .Both y=e^x and y=e^-2x are solutions. (Check this!)

4. If the discriminant c₁²-4c₀ is negative, then the equation $\lambda^2 + c_1\lambda + c_0 = 0$ has no solutions, unless we enlarge the number field to include $i=\sqrt{-1}$ ,i.e. unless we work with complex numbers. If c₁²-4c₀=-k² (we can writeany positive number as k²!) then ik is a square root of c₁²-4c₀since (ik)² = i²k² = (-1)k² = -k². The solutions of the associatedalgebraic equation are then

$\begin{displaymath}\lambda_1 = \frac{\textstyle -c_1 + ik}{\textstyle 2},~~\lambda_2 = \frac{\textstyle -c_1 - ik}{\textstyle 2}.\end{displaymath}$

Example 3. If we start with the differential equationy''+y=0 (so c₁=0 and c₀=1) the discriminant is c₁²-4c₀=-4, so 2i is a square root of the discriminant and the solutions of thecharacteristic equation are $\lambda_1 = i$ and $\lambda_2 = -i$ .

Example 4. If the differential equation is y''+2y'+2y=0 (so c₁=2 and c₀=2 and c₁²-4c₀=4-8 =-4). In thiscase the solutions of thecharacteristic equation are $\lambda = (-2\pm2i)/2$ ,i.e. $\lambda_1 = -1+i$ and $\lambda_2 = -1-i$ .

5. Going from the solutions of the characteristic equationto the solutions of the differential equation involves interpreting $e^{\lambda x}$ as a function of x when $\lambda$ is a complex number.Suppose $\lambda$ has real part a and imaginary part ib, so that $\lambda = a+ib$ with a and b real numbers. Then

$\begin{displaymath}e^{\lambda x} = e^{(a+ib)x} = e^{ax}e^{ibx}\end{displaymath}$

assuming for the moment that complex numbers can be exponentiated so asto satisfy the law of exponents. The factor e^ax does not causea problem, but what is e^ibx? Everything will work out if we take

$\begin{displaymath}e^{ibx} = \cos (bx) + i\sin(bx),\end{displaymath}$

and we will see later that this formula is a necessary consequence ofthe elementary properties of the exponential, sine and cosine functions.

6. Let us try this formula with our examples.

Example 3. For y''+y=0 we found $\lambda_1 = i$ and $\lambda_2 = -i$ ,so the solutions are y₁=e^ix and y₂=e^-ix.The formula gives us $y_1=\cos x + i\sin x$ and $y_2=\cos x - i\sin x$ .

Now here is a useful fact about linear differential equations: if y₁and y₂ are solutions of the homogeneous differential equationy''+c₁y'+c₂y=0, then so is the linear combination p y₁ + q y₂ for any numbers p and q. This fact is easy to check (just plug p y₁ + q y₂ into the equation and regroup terms; note that the coefficients a₁ and a₀ do not need to be constant for this towork, that p and q can be complex as well as real constants, andthat this works for equations af any order).

Using this fact with the solutions from our example, we notice that $\frac{1}{2}(y_1+y_2) = \cos x$ and $\frac{1}{2i}(y_1-y_2) = \sin x$ are both solutions. When we are given a problem with realcoefficients it is customary, and always possible, to exhibit realsolutions. Using the fact about linear combinations again, we can saythat $y=p\cos x + q\sin x$ is a solution for any p and q. Thisis the general solution. (It is also correct to call y=p e^ix +q e^-ix the general solution; which one you use depends on the context.)

Example 4. y''+2y'+2y=0. We found $\lambda_1 = -1+i$ and $\lambda_2 = -1-i$ .Using the formula we have

$\begin{displaymath}y_1 = e^{\lambda_1x}=e^{(-1+i) x}=e^{-x}e^{ix}=e^{-x}(\cos x + i\sin x),\end{displaymath}$

$\begin{displaymath}y_2 = e^{\lambda_2x}=e^{(-1-i) x}=e^{-x}e^{-ix}=e^{-x}(\cos x - i\sin x).\end{displaymath}$

Exactly as before we can take $\frac{1}{2}(y_1+y_2)$ and $\frac{1}{2i}(y_1-y_2)$ to get the real solutions $e^{-x}\cos x$ and $e^{-x}\sin x$ .(Check thatthese functions both satisfy the differential equation!) The generalsolution will be $y = p e^{-x}\cos x + q e^{-x}\sin x$ .

7. Repeated roots. Suppose the discriminant is zero:c₁²-4c₀ =0. Then the characteristic equation $\lambda^2 + c_1\lambda + c_0 = 0$ has one root. In this case both $e^{\lambda x}$ and $x e^{\lambda x}$ are solutions of the differential equation.

Example 5. Consider the equation y''+4y'+4y=0. Herec₁ = c₀ = 4. The discriminant is $c_1^2-4c_0 = 4^2-4\times 4 = 0$ .The only root is $\lambda = -2$ .Check that both e^-2x andx e^-2x are solutions. The general solution is theny = p e^-2x + q x e^-2x.

8. Initial Conditions. For a first-orderdifferential equation the undetermined constant can be adjusted tomake the solution satisfy the initial condition y(0)=y₀; in thesame way the p and the q in the general solution of a secondorder differential equation can be adjusted to satisfy initialconditions. Now there are two: we can specify both the value andthe first derivative of the solution for some ``initial'' valueof x.

Example 5. Suppose that for the differentialequation of Example 2, y''+y'-2y=0, we want a solution withy(0)=1 and y'(0)=-1. The general solution is y=p e^x + q e^-2x, since the two roots of the characteristicequation are 1 and -2. The method is to write down what theinitial conditions mean in terms of the general solution, and thento solve for p and q. In this case we have

$\begin{displaymath}1 = y(0)=p e^0 + q e^{-2\times 0} = p + q\end{displaymath}$

$\begin{displaymath}-1 = y'(0)=p e^0 -2 q e^{-2\times 0} = p -2q.\end{displaymath}$

This leads to the set of linear equations p + q = 1, p -2q = -1with solution q = 2/3, p = 1/3. Check that the solution $y = \frac{1}{3}e^x + \frac{2}{3}e^{-2x}$ satisfies the initialconditions.

Example 6. For the differential equation of Example 4, y''+2y'+2y=0, we found the general solution $y = p e^{-x}\cos x + q e^{-x}\sin x$ .To find a solutionsatisfying the initial conditions y(0)=-2 and y'(0)=1 we proceed as in the last example:

$\begin{displaymath}-2 = y(0) = p e^{-0}\cos 0 + q e^{-0}\sin 0 = p\end{displaymath}$

$\begin{displaymath}1 = y'(0)= -p e^{-0}\cos 0 -p e^{-0}\sin 0 -q e^{-0}\sin 0 + qe^{-0}\cos 0=-p +q.\end{displaymath}$

So p = -2 and q = -1. Check that the solution $y=-2e^{-x}\cos x-e^{-x}\sin x$ satisfies the initialconditions.

Tony Phillips
Math Dept, SUNY at Stony Brook

1998-11-30