INTEGER AND RATIONAL NUMBERS
Theorem 7.5 If a, b, c, d ∈ Z with c ≠ 0 and d > 0, then
i. a = b ![]() a + c = b +
c.
a + c = b +
c.
ii. a = b ![]() ac = bc.
ac = bc.
iii. a < b ![]() a + c < b
+ c.
a + c < b
+ c.
iv. a < b ![]() ad < bd.
ad < bd.
Proof Let 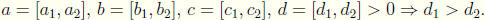
i.
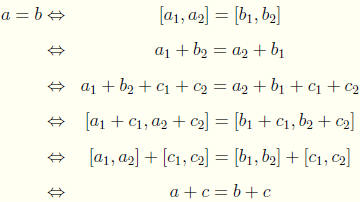
ii.
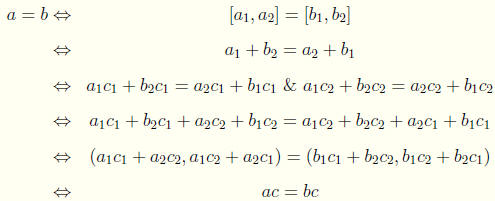
iii.
iv.
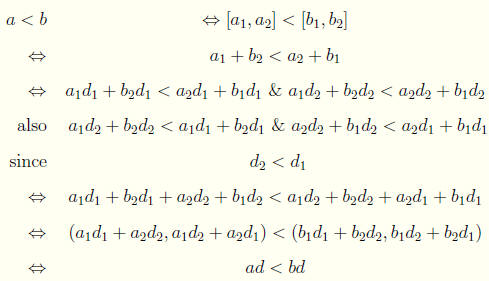
Definition An injection of a set a into a
set b is a bijection from a to a
subset of b. We will use the symbol , to
indicate that a map is an injection.
to
indicate that a map is an injection.
There is a natural injection, J, from N to Z defined by
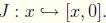
When there exists an injection from one set to another that preserves
order and arithmetic properties, we say the first set is embedded into
the
second. It is easy to verify that the natural injection is an embedding.
Lemma 7.6 If [a, b] is an integer, then there exists a natural number c ,
such that [a, b] = [c, 0], or [a, b] = [0, c].
Proof By trichotomy, either a > b, a = b, or a < b. If a > b let c be
such
that b + c = a, thus [a, b] = [c, 0]. If a = b let c = 0 (recall for us that 0
is a natural number), thus [a, b] = [0, 0] = [c, 0]. If a < b let c be such that
a + c = b, thus [a, b] = [0, c].
When a + c = b, and a, b, c ∈ N, we ex press c as b - a.
It is convenient to represent an equivalence class by one of its elements.
When a choice function is defined to choose from each of the equivalence
classes a representative element, that element is known as the canonical
representative.
For the integers we define our choice function to be
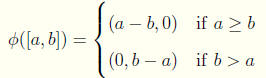
Thus every integer can be represented by [a, 0] or [0, a].
When the num-
bers are understood to be integers we will use a to represent [a, 0] and -a to
represent [0, a]. As an exercise the reader may wish to show that a > 0, and
-a < 0, that is [a, 0] > [0, 0], and [0, a] < [0, 0].
Definition The set of integers strictly greater than 0 is called the
Positive
Integers and are denoted by  . Those
integers strictly less than 0 are called
. Those
integers strictly less than 0 are called
the Negative Integers and are denoted by 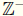 .
.
An Integral Domain
We leave it the reader to verify the fol lowing properties for Z.
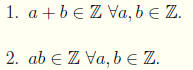
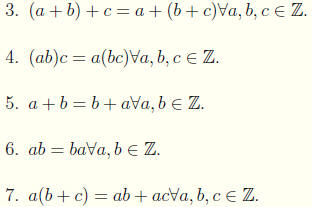
8.  such that a + e = e
+ a =
such that a + e = e
+ a = 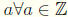
9. 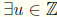 such that au = ua =
such that au = ua =
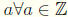
10. 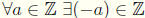 such that a + (¡a) = (¡a) + a = 0
such that a + (¡a) = (¡a) + a = 0
11*. If ab = 0, then either a = 0, or b = 0.
Properties 1 and 2 are called the closure properties, for
addition and mul -
tiplication respectively, properties 3 and 4 are the associative properties, 5
and 6 are the commutative properties. Property 7 is the distributive prop -
erty, we say multiplication distributes over addition. In properties 8 and 9
e and u are called the identities (again additive identity and multiplicative
identity respectively). The -a in property 10 is called the additive inverse,
or opposite. We say that a number a is a zero divisor if ab = 0, but neither
a nor b equal 0 (of course b is also a zero divisor ). Property 11* is called the
"no zero divisors" property.
Definition Any set with two binary operations satisfying these 11 proper-
ties is called an Integral Domain.
Rational Numbers
Another question we may wish to answer is: Two times what number is
1? This can be represented symbolically by 2x = 1. Again this question has
a vacant answer in the set of integers.
We extend the integers to the set of rational numbers by defining the
appropriate equivalence relation on the cartesian product of the integers with
themselves. We use the bold face letter Q to represent rational numbers.
The letter Q comes from the term quotient , i.e., the rational numbers are a
collection of quotients.
Definition The rational numbers are the collection of equivalence
classes
of Z × (Z - { 0} ) with respect to the equivalence relation
(x, y) ≡ (z,w) ![]() xw =
yz.
xw =
yz.
From the above comment we can see the rationale for this definition.
Using our previous notion of quotients we see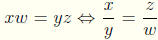 provided
provided
y,w ≠ 0. The reader should again verify that the relation is an equivalence
relation.
If we let a, b ∈ Z such that a ≥ 0 and b > 0, then the reader should
verify that [-a,-b] ≡ [a, b] and [a,-b] ≡ [-a, b]. Thus we may (and shall)
as sume for any rational number [a, b] that b > 0. Let d be the least element
of { y l (x, y) ∈ [a, b] and b > 0 }. We then let the unique element (c,
d) ∈ [a, b]
be the canonical representative of the rational number [a, b].
We again have the natural order defined on the rational numbers given
by
[x, y] < [z,w] iff xw < yz.
| Prev | Next |
