INTERMEDIATE ALGEBRA
COURSE DESCRIPTION: (750 characters, maximum)
A course designed for students with strong arithmetic
skills (without requiring a calculator) and an algebra
background, including solving linear equations in one variable and factoring
polynomials. This course will
extend students’ algebra skills to include solving radical, rational, quadratic,
& absolute-value equations,
and recognizing relationships between radical expressions and rational
exponents . Complex numbers are
introduced in this course as well. Problem solving involving real-life scenarios
is an integral part of this
course. In this course, students will enhance their problem-solving abilities
and their ability to communicate
concepts of algebra in the language of mathematics , both orally and written.
UNIT TITLES
1. Algebra Review (OPTIONAL)
2. Compound Linear Inequalities in One Variable
3. Linear Equations in Two Variables : Algebra, Geometry, and Modeling
4. Systems of Linear Equations
5. Linear Absolute-Value Equations in One Variable
6. Polynomial Expression Factoring Review
7. Rational Expressions & Equations
8. Radical Expressions & Equations
9. Complex Numbers
10. Quadratic Equations
11. Introduction to Functions and Function Notation (OPTIONAL)
ASSESSMENT: Please provide a brief description (250 characters maximum) that details how students will be assessed on the course outcomes.
Written Quizzes/Examinations.
Cumulative Final Examination.
*** Complete the following only if course is seeking general education status ***
GENERAL EDUCATION Competencies and Skills *:
Please highlight in green font all Competencies /
Skills from the list below that apply to this course. In the box to the
right of the
Competency/Skill, enter all specific learning outcome numbers (i.e. 1.1, 2.7,
5.12) that apply.
| 1. Read with critical comprehension | |
| 2. Speak and listen effectively | |
| 3. Write clearly and coherently | |
| 4. Think creatively, logically, critically,
and reflectively (analyze, synthesize, apply, and evaluate) |
2.1, 3.2, 3.5, 3.7, 3.9, 3.10, 3.14, 4.2, 4.4, 4.5, 4.6, 4.7, 5.2, 5.3, 5.4, 6.1, 6.2, 6.3, 6.4, 6.5, 6.6, 6.7. 6.9, 7.2, 7.3, 7.4, 7.5, 7.6, 7.7, 7.8, 7.9, 7.10, 7.11, 7.12, 8.3, 8.5, 8.6, 8.7, 8.9 8.10, 8.11, 8.12, 8.13, 8.14, 9.2, 9.3, 9.5, 9.6, 10.3, 10.4, 10.5, 10.,7, 10.8 |
| 5. Demonstrate and apply literacy in its
various forms: (highlight in green ALL that apply) ( 1. technological, 2. informational, 3. mathematical, 4. scientific, 5. cultural, 6. historical, 7. aesthetic and/or 8. environmental ) |
|
| 6. Apply problem solving techniques to
real-world experiences |
2.3, 3.8, 3.15, 4.8, 10.9, 10.11 |
| 7. Apply methods of scientific inquiry | |
| 8. Demonstrate an understanding of the
physical and biological environment and how it is impacted by human beings |
|
| 9. Demonstrate an understanding of and
appreciation for human diversities and commonalities |
|
| 10. Collaborate with others to achieve common goals. | |
| 11. Research, synthesize and produce original work | |
| 12. Practice ethical behavior | |
| 13. Demonstrate self-direction and self motivation | |
| 14. Assume responsibility for and understand
the impact of personal behaviors on self and society |
|
| 15. Contribute to the welfare of the community |
* General Education Competencies and Skills endorsed by ’05-’06 General Education Task Force
| Unit 1 | Algebra Review (OPTIONAL) | |
| General Outcome: | ||
| 1.0 | The student shall be able to (1) solve linear equations in one variable (including proportions and literal equations), (2) solve linear inequalities in one variable (including compound inequalities), (3) recognize when a given equation or inequality has no solution, (4) solve appropriate word problems involving linear equations and inequalities in one variable, and (5) define terminology associated with polynomials. | |
| Specific Measurable Learning Outcomes: Upon successful completion of this unit, the student shall be able to: | ||
| 1.1 | Define the terms “variable,” “coefficient,” “expression,” and “equation.” | |
| 1.2 | Explain what it means to be a solution to an equation or inequality in one variable. | |
| 1.3 | Determine if a given variable value is a solution to an equation or inequality. | |
| 1.4 | Solve one- step and multi -step linear equations in one variable, including those with variables on both sides of the equal sign and those requiring use of the distributive property. | |
| 1.5 | Identify linear equations in one variable as conditional, a contradiction, or an identity. | |
| 1.6 | Solve proportionalities. | |
| 1.7 | Solve appropriate algebraic and geometric word problems by modeling them with linear equations in one variable or proportionalities. | |
| 1.8 | Solve literal equations for a specified variable | |
| 1.9 | Solve one-step and multi-step linear inequalities in one variable, including those with variables on both sides of the inequality sign and those requiring use of the distributive property . | |
| 1.10 | Present solutions to linear inequalities in one variable in three ways: Inequality notation, interval notation, and graphically on a number line. | |
| 1.11 | Solve appropriate word problems by modeling them with linear inequalities in one variable. | |
| 1.1 | Define the terms “polynomial,” “leading coefficient (of a polynomial),” and “degree (of a polynomial).” | |
| Unit 2 | Compound Linear Inequalities in One Variable | |
| General Outcome | ||
| 2.0 | The student shall be able to solve compound linear inequalities in one variable (including compound inequalities), and present solutions using inequality notation, interval notation, and graphic notation. | |
| Specific Measurable Learning Outcomes: Upon successful completion of this unit, the student shall be able to: | ||
| 2.1 | Solve AND and OR compound linear inequalities in one variable (including three-part inequalities). | |
| 2.2 | Present solutions to compound linear inequalities in one variable in three ways: Inequality notation, interval notation, and graphically on a number line. | |
| 2.3 | Solve appropriate word problems by modeling them with compound linear inequalities in one variable. | |
| Unit 3 | Linear Equations in Two Variables: Algebra, Geometry, and Modeling | |
| General Outcome: | ||
| 3.0 | The student shall be able to (1) write equations and sketch graphs of linear equations in two variables, given appropriate information, (2) model real-world scenarios using linear equations in two variables, and (3) graph linear equations in two variables. | |
| Specific Measurable Learning
Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 3.1 | Explain what it means to be a solution to an equation in two variables. | |
| 3.2 | Determine if a given ordered pair is a solution to an equation in two variables. | |
| 3.3 | Define the terms “x- (or horizontal) intercept” and “y- (or vertical) intercept.” | |
| 3.4 | Sketch the graphs of linear equations in two variables given any two points. | |
| 3.5 | Identify and determine the x- and y-intercepts of graphs of linear equations in two variables. | |
| 3.6 | Define the term “slope.” | |
| 3.7 | Evaluate the slopes of horizontal, vertical, and diagonal lines given a graph, two points, or the equation of the line. | |
| 3.8 | Interpret the practical meaning of linear slope in appropriate word problems. | |
| 3.9 | Determine the equations of horizontal and vertical lines, given a graph, the slope and a point, or two points. | |
| 3.10 | Determine the equation of lines, in “slope-intercept” form, “point-slope” form, and “standard” form, given the slope and a point or two points. | |
| 3.11 | Sketch graphs of diagonal, horizontal, and vertical lines given the equation or other appropriate information (e.g. two points; the slope & a point). | |
| 3.12 | Define the terms “parallel lines” and “perpendicular lines.” | |
| 3.13 | Explain the relationships between the slopes of parallel and perpendicular lines, and determine whether any pair of given linear equations in two variables represent parallel lines, perpendicular lines, or neither. | |
| 3.14 | Determine the equation of parallel and perpendicular lines, given appropriate information. | |
| 3.15 | Solve appropriate word problems by modeling them with linear equations in two variables. | |
| Unit 4 | Systems of Linear Equations | |
| General Outcome: | ||
| 4.0 | The student shall be able to solve systems of linear equations graphically and algebraically (using the methods of elimination and substitution), and solve word problems by modeling them with systems of linear equations. | |
| Specific Measurable
Learning Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 4.1 | Explain what it means to be a solution to a system of linear equations. | |
| 4.2 | Determine if a given ordered pair is a solution to a system of linear equations. | |
| 4.3 | Define the terms “consistent system,” “inconsistent system,” “dependent system,” and “independent system.” | |
| 4.4 | Determine graphically if a system of linear equations is consistent, inconsistent, or dependent. | |
| 4.5 | Solve systems of linear equations by graphing. | |
| 4.6 | Solve systems of linear equations using the elimination method (i.e. addition method). | |
| 4.7 | Solve systems of linear equations using the substitution method. | |
| 4.8 | Solve appropriate word problems by modeling them with systems of linear equations. | |
| Unit 5 | Linear Absolute-Value Equations in One Variable | |
| General Outcome: | ||
| 5.0 | The student shall be able to solve linear absolute-value equations in one variable. | |
| Specific Measurable
Learning Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 5.1 | Define the term “absolute value.” | |
| 5.2 | Solve absolute value equations of the form |ax + b| = k, for k ≥ 0. | |
| 5.3 | Explain why absolute value equations of the form |ax + b| = k, for k < 0, have no solution. | |
| 5.4 | Solve absolute value equations of the
form
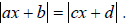 |
|
| Unit 6 | Polynomial Expression Factoring Review | |
| General Outcome: | ||
| 6.0 | The student shall be able to factor polynomial expressions using a variety of methods. | |
| Specific Measurable
Learning Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 6.1 | Factor the GCF of polynomials’ terms. | |
| 6.2 | Factor -1 from polynomials with negative leading coefficients. | |
| 6.3 | Factor polynomial expressions by pairwise grouping. | |
| 6.4 | Factor binomial expressions that are differences of perfect squares. | |
| 6.5 | Factor binomial expressions that are sums and differences of perfect cubes. | |
| 6.6 | Factor appropriate trinomial expressions into a product of binomials. | |
| 6.7 | Factor perfect square trinomial expressions. | |
| 6.8 | Define the term “prime polynomial.” | |
| 6.9 | Determine whether polynomial expressions are prime or factorable. | |
| Unit 7 | Rational Expressions & Equations | |
| General Outcome: | ||
| 7.0 | The student shall be able to simplify rational expressions and solve rational equations. | |
| Specific Measurable
Learning Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 7.1 | Define the term “rational expression.” | |
| 7.2 | Determine value(s) of the variable for which rational expressions are undefined. | |
| 7.3 | Simplify rational expressions by canceling common monomial and binomial factors of the numerator and denominator . | |
| 7.4 | Determine the least common denominator of rational expressions. | |
| 7.5 | Add and subtract rational expressions with the same and with different denominators . | |
| 7.6 | Multiply and divide rational expressions. | |
| 7.7 | Simplify complex rational expressions with positive exponents only by rewriting as a multiplication problem. | |
| 7.8 | Simplify complex rational expressions with positive exponents only using the LCD method. | |
| 7.9 | Simplify complex fractions containing terms with negative exponents. | |
| 7.10 | Solve rational equations. | |
| 7.11 | Solve literal equations containing rational expressions. | |
| 7.12 | Determine whether or not a solution to a rational equation is extraneous | |
| 7.13 | Solve appropriate word problems by modeling them with rational equations. (OPTIONAL) | |
| Unit 8 | Radical Expressions & Equations | |
| General Outcome: | ||
| 8.0 | The student shall be able to
simplify, and perform operations on radical expressions, rationalize
radical components of rational expressions, solve appropriate radical
equations, and convert between radical expressions and expressions with a rational exponent. |
|
| Specific Measurable Learning Outcomes: Upon successful completion of this unit, the student shall be able to: | ||
| 8.1 | Define the terms “square root,” “principal square root,” “radical,” and “radicand.” | |
| 8.2 | Define the terms “nth root” and “index.” | |
| 8.3 | Simplify radical expressions with any root (both numerical and variable expressions). | |
| 8.4 | Explain why any even root of a negative number is not a real number , but any odd root of a negative number is a real number. | |
| 8.5 | Add, subtract, multiply, and divide radical expressions (both numerical and variable expressions). | |
| 8.6 | Rationalize the denominator of rational expressions having a radical term (either a radical monomial or a binomial with a radical term). | |
| 8.7 | Rationalize the numerator of rational expressions having a radical factor (either a radical monomial or a binomial with a radical term). (OPTIONAL) | |
| 8.8 | Explain the relationship between a radical and a rational exponent. | |
| 8.9 | Express radical expressions using rational exponent notation, and vice versa. | |
| 8.10 | Apply the rules of exponents to simplify expressions with rational exponents. | |
| 8.11 | Solve appropriate radical equations (including double-radical equations), excluding those requiring double squaring. | |
| 8.12 | Determine whether or not a solution to a radical equation is extraneous. | |
| 8.13 | Solve literal equations that contain radicals | |
| 8.14 | Solve literal equations that require
use of the Square Root Property (e.g. Solve ,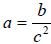 ,for
c). ,for
c). |
|
| Unit 9 | Complex Numbers | |
| General Outcome: | ||
| 9.0 | The student shall be able to write square roots of negative numbers as imaginary numbers, and perform operations on complex numbers. | |
| Specific Measurable
Learning Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 9.1 | Define the terms “imaginary number” and “i.” | |
| 9.2 | Simplify i2 as -1. | |
| 9.3 | Simplify expressions of the form
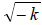 , where k > 0. , where k > 0. |
|
| 9.4 | Define the terms “complex number,” “real part (of a complex number),” and “imaginary part (of a complex number).” | |
| 9.5 | Express complex numbers in standard form, a + bi. | |
| 9.6 | Identify the real part and the imaginary part of complex numbers in standard form. | |
| 9.7 | Explain why all imaginary numbers are complex numbers, but not vice versa. | |
| 9.8 | Explain why all real numbers are complex numbers, but not vice versa. | |
| Unit 10 | Quadratic Equations | |
| General Outcome: | ||
| 10.0 | The student shall be able to solve quadratic equations by factoring, the square-root method, completing the square, and the quadratic formula , and solve word problems by modeling them with quadratic equations. | |
| Specific Measurable
Learning Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 10.1 | Define the terms “quadratic expression” and “quadratic equation.” | |
| 10.2 | Determine if a given polynomial expression or equation is quadratic. | |
| 10.3 | Solve quadratic equations (and other appropriate polynomial equations) having real solutions by factoring. | |
| 10.4 | Use the square root property to solve quadratic equations of the form a(bx + c)2+d = k, having real or complex solutions. | |
| 10.5 | Solve quadratic equations having real or complex solutions by completing the square. | |
| 10.6 | State, and explain the purpose of, the quadratic formula. | |
| 10.7 | Solve quadratic equations having real or complex solutions using the quadratic formula. | |
| 10.8 | Solve literal polynomial equations. | |
| 10.9 | Solve appropriate word problems by modeling them with quadratic (or other polynomial) equations. | |
| 10.10 | State the Pythagorean Theorem, and explain what it means. | |
| 10.11 | Solve appropriate Pythagorean Theorem-based word problems requiring quadratic equations. | |
| Unit 11 | Introduction to Functions and Function Notation (OPTIONAL) | |
| General Outcome: | ||
| 11.0 | The student shall be able to determine if relations given numerically, graphically, or algebraically are functions, express functions using function notation, evaluate functions, and determine the domains and ranges of functions. | |
| Specific Measurable
Learning Outcomes: Upon successful completion of this unit, the student shall be able to: |
||
| 11.1 | Define the terms “relation” and “function.” | |
| 11.2 | Determine if relations expressed as collections of ordered pairs are functions. | |
| 11.3 | Determine if relations expressed as mappings are functions. | |
| 11.4 | State, and explain the purpose of, the vertical line test. | |
| 11.5 | Use the vertical line test to determine if relations expressed as graphs are also functions. | |
| 11.6 | Express a functional relationship using function notation, y = f(x). | |
| 11.7 | Express linear equations in two variables using function notation. | |
| 11.8 | Explain why vertical lines are the only lines that are not functions. | |
| 11.9 | Define the terms “input (of a function)” and “output (of a function).” | |
| 11.10 | Evaluate functions (including constant functions) for specific domain values. | |
| Prev | Next |