Math 100 Practice Exam 3A Solutions
Solutions
1. This problem is very hard to typeset, but the answers are:
(a) Q(x) = x2 + 3x + 9 and R(x) = 7. To check, we compute
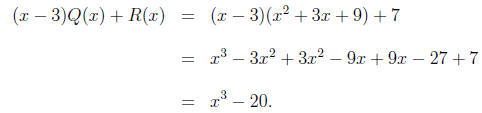
(b) Q(x) = 2x3+6x2-x-9 and R(x) = -20x+11. Again, to check, we compute
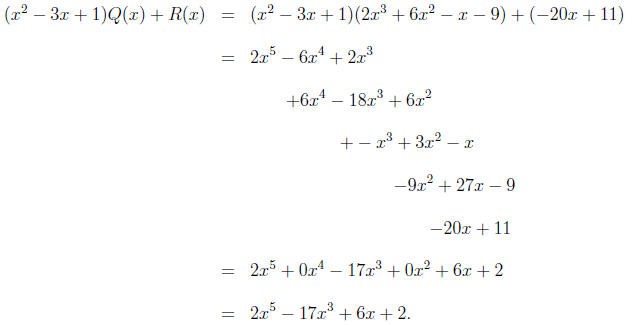
2. Let us construct a polynomial P (x), having the desired properties . First, we
note
that any polynomial with a factor of (x+1)2, will have a zero of multiplicity 2
at -1.
So, P should have a factor of (x+1)2. Now, if we want there to be a root at 2+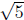
,
we should also have a factor of (x - (2 +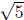
)).
In order that P (x) have rational
coefficients, we must have 2-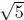
being a root of P(x), as well, so that (x-(2-
))
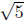is a factor of P(x). (See the boxed statements on page 317 for a precise
formulation
of this result.) Since P(x) is to have degree 4 and we have just determined 4
linear
factors, it must be that
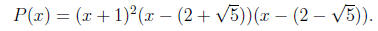
3. f(x) = 2x4 - x3 - 13x2 + 5x + 15.
(a) Since we are looking for rational zeros, it is reasonable to try to
implement
the rational zero theorem. This theorem states that if p/q is a zero of f(x),
where p
is relatively prime to q (i.e. have no common factors except -1 and 1) then p is
a
factor of the constant coefficient of f and q is a factor of the leading
coefficient of f.
So, we find the factors of the leading coefficient 2 and the constant
coefficient 15. 2
has factors ±1,±2 and 15 has factors ±1,±3,±5,±15. It follows that the possible
rational zeros of f are:
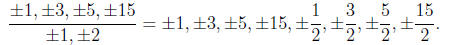
Among these possibilities, direct substitution shows that
-1 and 3/2 are the only ra-
tional zeros.
(b) Since -1 and 3/2 are zeros of f, we know that (x + 1)
and (x - 3/2)
are factors of f. That is, f(x) = (x + 1)(x - 3/2 )Q(x), for some polynomial Q(x).
If we can find
the zeros of Q(x), we will know all of the zeros of f(x). So, to find Q(x), we
use
long division to calculate f(x)/[(x + 1)(x - 3/2 )] = f(x)/(x2 - 1/2x - 3/2 ).
This gives
Q(x) = 2x2 - 10 = 2(x2 - 5). So, the remaining zeros of f(x) are when Q(x) =
0, or
equivalently , when x = ±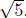
.
4. (i) f(x) = x4 + 5x3 + 6x2 = x2(x2 + 5x + 6) =
x2(x + 2)(x + 3)
(ii)
| Zero | Multiplicity |
| 0 | 2 |
| -2 | 1 |
| -3 | 1 |
5. f(x) = x4 + 3x3 - x - 3.
(a) By the rational zero test, we find that f has a zero at -3 and 1.
(b) Since f has zeros at -3 and 1, we see that (x + 3)(x - 1) = x2 + 2x - 3
must
divide f. Upon long division, we find that
f(x) = (x2 + 2x - 3)(x2 + x + 1):
(c) We already have two linear factors for f, namely, (x+3) and (x-1). To find
the others, we must find the roots of x2 +x+1. Unfortunately, we this does not
have
real roots, but the quadratic equation shows that the roots of x2 + x + 1 are
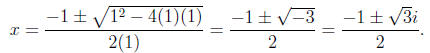
So, f factors into the following
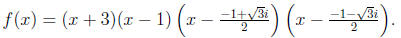
6. (a) Remember inequality signs change only when you
multiply or divide by a
negative .
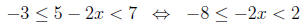( by subtracting 5)
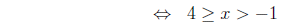(by dividing by -2)
In interval notation, this is the set (-1, 4].
(b)
In interval notation, this is the set (10/3,∞).
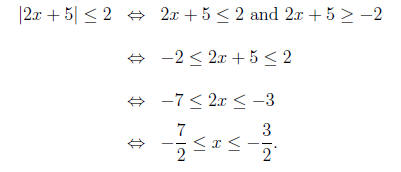
8. In general, a polynomial of degree n can have at most n x-intercepts (i.e.
zeros). If
we know in addition whether n is even or odd, we can get more information.
Namely,
if n is even, then the number of x -intercepts can be anywhere between 0 and n.
On
the other hand, if n is odd, then the number of x- intercepts will be between 1
and n.
The number of "turning points" can be anywhere between 0 and n - 1. If n is odd,
then
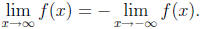If
n is even, then
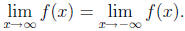
In our particular problem, the above statements imply that
f can have anywhere
between 1 and 23. f can have anywhere between 0 and 22 turning points. Since 23
is odd, f(x) → ∞ as x → -∞, we must have f(x) → -∞ as x → ∞.
9. Let us write
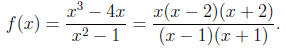
(a) f has zeros only when the numerator is zero and the denominator is nonzero .
These values are when x = 0,-2, 2. The y-intercept occurs when x = 0. In point
notation, the intercepts of f are (0, 0), (-2, 0), and (2, 0).
(b) Vertical asymptotes will occur for values of x when
the denominator is equal
to zero and the numerator is not. These are the lines x = -1 and x = 1.
Since the degree of the polynomial in the numerator is one greater than the
degree
of the polynomial in the denominator, we must have f having an oblique
asymptote.
That is, f is asymptotic to some line y = mx + b. (Note that this immediately
tells
us that there are no horizontal asymptotes.) To find this line, we use long
division
to find Q(x) and R(x) such that x3 - 4x = (x2 - 1)Q(x) + R(x). This process
gives
Q(x) = x and R(x) = -3x. The line y that f is asymptotic to is given by Q(x).
That is, f is asymptotic to the line y = x.
(c)
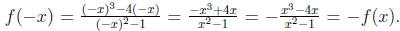So, f is symmetric about
the origin.
(d) f is positive in the intervals : (-2,-1), (0, 1) and (2,∞).
10. (a) Following the procedure outlined in 9b, we have
that f has an oblique as-
ymptote at the line y = x - 1 and a vertical asymptote at x = -2. Since f has an
oblique asymptote f can not have any horizontal asymptotes.
(b) g has a horizontal asymptote when y = 0, since the
degree of the numerator
is strictly less than the degree of the denominator. (In the even that the two
degrees
are equal, there will still be a horizontal asymptote and it will be at the line
y = a/b ,
where a is the leading coefficient of the polynomial in the numerator and b is
the
leading coefficient of the denominator.) There are two vertical asymptotes at x
=
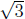
and x = -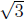
.
11. (a) f(x) → ∞ as x → -∞, since the degree of f is even
and the leading
coefficient is positive.
(b) g(x)→ -∞, since the degree of g is odd and the leading coefficient is
positive.
| Prev | Next |