Math Practice Problem Solutions

Explain in your words why having the formula

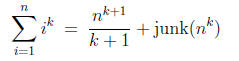
allows to evaluate

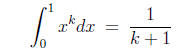
exactly.

Solution : We have done that in class. Written down briefly, we cans say that the
area under the curve y = f(x) (we may say this now after Descartes and Fermat)
can be estimated as follows (for a monotone function)

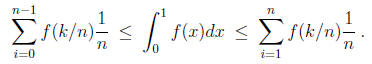
Now for f(x) = x^a, a any rational number we have

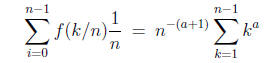
and in particular

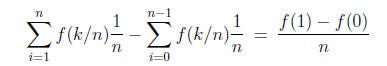
gets arbitrary small. So that definitely

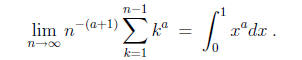
However,

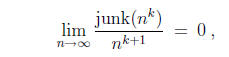
and hence

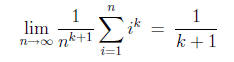
if and only if

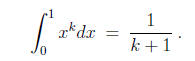
Find the correct value for C such that

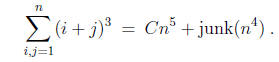
Hint: You may apply the “junk” rule n ^a junk(n^b) = junk(n^a+b).

Solution: We write
(i + j)³ = i³ + 3i²j + 3ij² + j³

and get

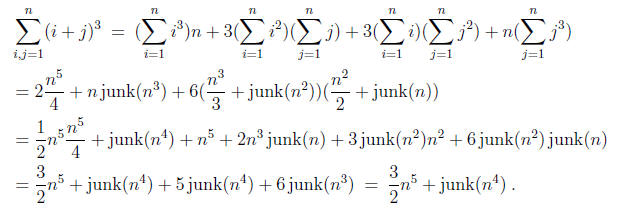
Thus C = 3/2 .
Calculate

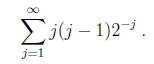
Find a geometric object which has this number as volume .
We have learned from Oresme that 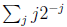corresponds to a 2-d object, summing
up blocks of length 1, 1/2, 1/4,..., We can take the same picture and add the third
component of height j −1 in the z- coordinate , say. This becomes an infinite sum of
rectangular prism, which I can not draw in this program. However, I can calculate
the sum:

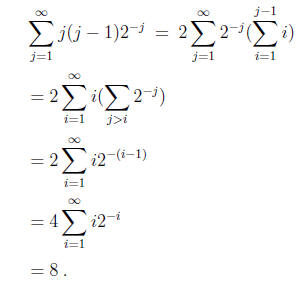
In the last line we used Oresme result.

What was lost and what was gained in the time frame described as medieval in the
book (say including Descartes and Fermat).

Certainly, the precision notion of ‘what is a proof’ was lost. Lets remember, Kepler
was so appalled from the reading of Archimedes book, and Euclid’s element, that
he didn’t think it was necessary to check whether his result could really obtained
from the greek method of inscribing and circumscribing polytopes.

What was certainly gained is the mathematical notation . After Descartes you can
fully do what corresponds high school algebra , solving quadratic equations, solving
a number of linear equations with not too many unknowns. We can also take about
the function f(x) = x^q and solutions to
x⁵ + y⁶ − z⁸ = 13 .

(Maybe also about 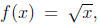or in general 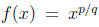(if we include Wallis
here-which is stretching the question!)

And any rate, we have a large reservoir on symbols , but very little theory to talk
about functions and their properties. Even calculating the first integrals was possible
(think of Fermat’s nice argument using infinite sums), and geometric series were
known and accepted. In the greek period there where probably known and not
accepted.

I am sure this is not complete, but I will send it out now.