The Pythagorean Theorem
TEACHING TIPS
| COMBINING LIKE TERMS – MISCONCEPTION ALERT | |
| Teaching Tip 1 Preview/Warmup |
Since the proof of the Pythagorean
theorem in this lesson requires some symbol manipulation, practice is provided in the warmup. Be prepared for student mistakes when combining like terms . If students falter by
stating that ab + ab = a2b2 , remind them of previous experiences with Later in the lesson, polygon cutouts link a visual
model to this symbol manipulation . |
| EXPLORING THE PYTHAGOREAN THEOREM AND ITS CONVERSE | |
| Teaching Tip 2 Practice |
In general, if we have a theorem that
says, “If A is true, then B is true”, then the converse of that statement is, “If B is true, then A is true.” Therefore, Pythagorean Theorem: If a triangle is a right
triangle, then the sum of the squares Converse of the Pythagorean theorem: If the sum of
the squares of the two Students can use the Pythagorean theorem together
with its converse to verify numerically |
| PREVIEW / WARMUP | |
Whole Class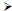 SP1, OH1 SP1, OH1Ready, Set, Go Teaching Tip 1 |
• Introduce the goals and standards
for the lesson. Underline important vocabulary. • Students find the areas of the
figures given and simplify the given |
| INTRODUCE 1 | |
| Whole Class
|
• Discuss basic properties of a right
triangle (three sides, two acute angles, one right angle) and vocabulary (legs, hypotenuse) associated with the naming of the sides of a right triangle.
Which side of a right triangle must be the longest?
Why? The • Focus attention on the small triangle on the
left. Demonstrate how to What is the area of the square on the shorter leg?
9 square units on How do the side lengths relate to the areas of
these squares? Side • Demonstrate how to draw a square on the
hypotenuse using the given What steps can be taken to find the area of Once you know the area of the square on |
| EXPLORE 1 | |
| Pairs/ Individual
|
• Students find the area of the
square on the hypotenuse for the small triangle and then find the length of the hypotenuse by taking its square root. Ask questions to guide computation as needed.
What is the area of the large square? 49 sq units The
area of each How are the areas of the squares on the legs
related to the area of • Students find lengths of sides and areas of
squares on the sides for the |
| SUMMARIZE 1 | |
| Whole Class
|
• Invite students to explain their
work and calculations on the overhead or board, leading them to conjecture the Pythagorean theorem based on two numerical illustrations . What appears to
be a relationship between the area of the square • Explain to students that this conjecture is
among the most well known |
| INTRODUCE 2 | |
| Whole Class
R1 |
• Lead students through a cut-up
proof of the Pythagorean theorem. Show how each of the squares was constructed using side lengths from the right triangle. Label some right angles and lengths.
What does it mean to say that two shapes are
congruent? They have Are the two large shapes congruent? Yes. How do
you know? They How do their areas compare? They are same. • Write the area inside each triangle, rectangle, and square. • Cut out both squares, and cut them into the smaller polygons. • Arrange two triangles to form a rectangle. What does this mean geometrically? The area of two
triangles is the same • Separate the cut up pieces into two piles,
keeping dissected pieces from What equation is illustrated? • Have students rearrange pieces so that the
pieces with equal area are What simplified equation does the picture suggest?
|
| EXPLORE 2 | |
| Individual/Pairs
|
• Students answer questions that lead
them to record for themselves this common proof of the Pythagorean theorem. Circulate as students work, giving reminders and hints only if needed. |
| SUMMARIZE 2 | |
| Whole Class
Math Background 1 |
• Ask individuals or pairs to come to
the overhead to explain the different parts of the problem. • Congratulate students for proving the Pythagorean theorem. What is the Pythagorean theorem? For a right triangle, the sum of the • Using one triangle and the three squares,
arrange the pieces to show |
| PRACTICE | |
| Individuals
Teaching Tip 2 |
• This group of problems uses both
the Pythagorean theorem and its converse. Use for additional practice or homework. |
| EXTEND | |
| Whole Class Math Background 2 |
• Share the Garfield proof of the
Pythagorean theorem with students if desired. |
| CLOSURE | |
| Whole Class
|
• Review the goals and standards for the lesson. |
SP1-Ready Set Go
1. 48 sq. units
2. xy sq. units
3. 24 sq. units
4. 1/2xy sq. units.
5. a+a=2a
6. ab+ab=2ab
7. (1/2)a+(1/2)a = a
8. (1/2)ab+(1/2)ab=ab
SP2—Two Right Triangles
1. 3, 4
2. 4, 7
3. 9, 16
4. 16, 49
5. 25, 65
6. 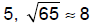
7. In a right triangle, the area of the square on the hypotenuse is equal to the
sum
of the areas of the squares on the two legs.
SP5—Right Triangle ABC
3. In a right triangle, the square of the length of the
hypotenuse is equal to the
sum of the squares of the lengths of the legs.
4. Pythagorean theorem
SP6-7—Pythagorean Theorem Practice
1. 9 + 4 = 13; 32 + 22 = ( 13)2
2. 4 squared + 5 squared does not equal 9 squared. 16+25 does not equal
81.
3. 13
4. no
5. 3-4-5, 6-8-10
6. only the 6-8-10 triangle is a right triangle, by the converse to the
Pythagorean
Theorem. The 4-6-8 triangle is not a right triangle, by the Pythagorean theorem.
7. This cannot be right because of the converse to the Pythagorean Theorem. The
given triangle is not a right triangle. Note: The Pythagorean Theorem itself
does not
justify Tommy’s answer. The converse to the Pythagorean Theorem goes beyond
that, saying that Tommy’s answer also cannot be a lucky guess
| Prev | Next |
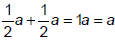 might represent the cost of two
halves of apples, which is the cost of one
might represent the cost of two
halves of apples, which is the cost of one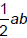 , and the area of each
, and the area of each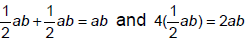
 SP2, OH2
SP2, OH2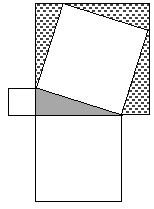
 SP2
SP2 SP2, OH2
SP2, OH2 SP3-4
SP3-4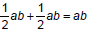
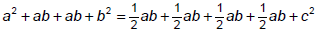
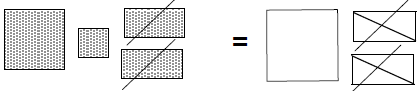
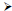 SP3-4
SP3-4 SP5, OH
SP5, OH SP6-7
SP6-7 SP1, OH1
SP1, OH1