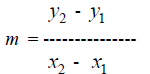MATH STUDY GUIDE
SLOPE
| The slope of a line can be determined in two
ways . 1) If you know the equation of the line , solve it for y. The slope is the coefficient of x. 2) If you know the coordinates of two points, 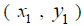 and and
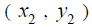 use the formula: use the formula:
|
Sec. 4.3, 4.4 |
SIMPLIFY
Fractions: If there are no variables, see compute.
| 1 | To add or subtract : a) Find the Lowest Common Denominator. b) Change each fraction to an equivalent fraction by multiplying numerator and denominator by the same value. c) Add the numerators and use the common denominator. If there is a “—“ in front of a fraction be sure to distribute it to EVERY TERM in the numerator. |
Sec. 8.3, 8.4 |
| 2 | To multiply, factor numerators and denominators reducing where possible. Leave the answer in factored form unless it is part of a larger problem. (i.e. must be added to other terms.) | Sec. 8.2 |
| 3 | To divide, FIRST invert the divisor, and then proceed as in multiplication. | Sec. 8.2 |
| 4 | If there is a fraction within a numerator or denominator, either: | |
| a) Multiply numerator and denominator of the largest fraction by the LCD for all fractions | Sec. 8.5 | |
| OR | ||
| b) Treat numerator and denominator as a grouping and simplify, then divide as indicated by the larger fraction. | Sec. 8.5 | |
| 5 | Remember, no denominator of any fraction may ever be zero. | Sec. 8.1 |
| 6 | Always reduce final answers where possible by dividing common factors from numerator and denominator. | Sec. 8.1 |
Radicals
| 1 | Is the expression under the radical a perfect square? Simplify. | Sec. 9.1 |
| 2 | Is there a factor of the expression under the radical that is a perfect square? Factor it out and simplify. | Sec. 9.2 |
| 3 | Is there a fraction under the
radical? Simplify the expression into a single fraction and separate into two separate radicals. |
Sec. 9.2 |
| 4 | Is there a product or quotient of radicals? Perform the operations. |
Sec. 9.2 |
| 5 | Are two radicals in a sum alike (same index and
radicand?) Add using the coefficients of the radicals. |
Sec. 9.3 |
| 6 | Is there a radical in a denominator? | |
| Rationalize it : | ||
| a) If it is a single radical, multiply numerator and denominator by that radical. | Sec. 9.4 | |
| b) If there is a sum or two terms where one or both are radicals multiply the numerator and denominator by the CONJUGATE of the denominator. (The conjugate is formed by using the same two terms but changing the sign between them.) | Sec. 9.4 |
| You may apply any appropriate rule to
the expression, but the following strategies may be useful: a) Are there powers of other expressions? Use the Power (of a Product) rule to remove parentheses . b) Are there powers of exponential expressions? Use Power (of a Power) rule where appropriate. c) Are there like bases in numerator or denominator? Use the product rule to simplify (add exponents.) d) Are there like bases in both numerator and denominator? Divide (by subtracting exponents.) e) Are there negative exponents ? Use the negative exponent rule to write the reciprocal. f) Write as a single fraction. g) Are you finished? Each exponent should apply to a single base. Each base should appear only once. There should be no negative exponents. Powers of numbers should be calculated . The fraction should be in lowest terms. |
Sec. 6.2, |
Scientific Notation
| Numbers written in Scientific Notation are in the
form (a number between 1 and 10) (a power of 10.) - To multiply or divide numbers written in scientific notation: 1) Multiply or divide the coefficients 2) Use the rules of exponents to multiply or divide the powers of 10. 3) Check to be sure the new coefficient is between 1 and 10. If not, rewrite it in Scientific Notation and simplify the powers of 10. |
Sec 6.7 |
FACTOR
To factor a number means to write it as a product of primes (numbers that cannot be factored further.) Begin with any product and then break each number down until none can be factored further.
| To factor a polynomial: | Sec. 7.5 |
| 1) Is there a factor common to all terms? Factor out the greatest common factor (term.) | Sec. 7.1 |
| 2) Are there 4 terms? Try factoring by grouping | Sec. 7.1 |
| 3) Is there a common pattern? a) Is this a difference of 2 squares? b) Is this a perfect square trinomial ? c) Is this the sum or difference of two cubes ? |
Sec. 7.4 |
| When all else fails on a trinomial : 4) Try splitting the middle term into two and factoring by grouping. OR |
Sec. 7.3 |
| 5) Perform a structures search. (This
is an organized version of the trial factors from the text.) a) List all the possible ways to factor the first (squared) term. These are the column headings. b) In each column, list all the possible arrangements of the factors for the last (constant) term. (These form the rows.) c) Test each entry in your table using FOIL to see if this makes the middle term possible. (If there are no candidates, report that it DOES NOT FACTOR.) d) If you have a candidate, insert signs to try to match original. i. If the last sign (constant) is negative, the signs are different. ii. If the last sign is positive , the two signs are alike, Use the sign of the middle term. iii. If none of the above works, go on searching for new candidates. iv. If you exhaust the list and none work, report that it DOES NOT FACTOR. e) Check your solution. Check to be sure that none of the factors can be factored further. |
Sec. 7.2 |
WORD PROBLEMS
| “How to Solve Word Problems in
Algebra” By Mildred Johnson is an excellent and inexpensive resource. It
is available in the bookstore. 1) Read
through the problem to determine type. |
|
| 4) Pick out the basic unknown and
finish the above sentence. 5) Write as many other quantities as possible in terms of x and label them. |
Sec. 2.5 |
| 6) Is there STILL another unknown? If
so, write, “Let y be …” and complete the sentence. Write all other
quantities in terms of ‘x and y’. You may need one or more of the
formulas below to complete this. Note: Tables are useful in many of these problems. Make one like the models in the text where appropriate. |
Sec. 5.4 |
| 7) Write any formula(s) that apply to this type of problem. | |
| a) d = rt (distance, time and speed) b) In wind or stream, when moving with the current, the speed is the sum of the speed of the craft and the current. |
Sec. 3.1 |
| c) i = Pr (interest for 1 year) | Sec. 3.1 |
| d) Concentration of a solution (%
target) (amount mixture) = amount target ingredient. e) (cost per item) (number of items) = value |
Sec. 3.1 |
| f) (denomination of a bill) (# of
bills) = value g) consecutive numbers x, x + 1, x + 2 , etc. h) consecutive ODD or EVEN numbers (The value of the first determines which) n, n + 2, n + 4 etc. i) In age problems, when they say “in 5 years,” write each age + 5 |
Sec. 2.5 |
| j) Work rate problems convert the time to do a job into the work done per time period by taking the reciprocal. THESE quantities can be added or subtracted. | Sec. 8.7 |
| k) Geometric formulas for the perimeter of a triangle and the sum of its angle. | Sec. 3.3 |
| l) In a triangle with a right angle, you may use the Pythagorean Formula. | Sec. 10.1 |
| m) Basic %, A = PB 8) Use the formula or the words from the problem to write an equation. 9) Solve the equation for x (or x and y.) 10) REREAD the question. Write all the quantities from the original problem using the value for x as a key. 11) Answer the question asked. 12) Check the answer with the problem’s original words. Discard any answers that don’t fit. |
Sec. 2.4 |
| Prev | Next |