Matrices

4.4. Special Matrices.

1. A square matrix is a matrix with the same number of rows as columns.

2. A diagonal matrix is a square matrix whose entries off the main diagonal are
zero.

3. An upper triangular matrix is a matrix having all the entries below the main
diagonal equal to zero.

4. A lower triangular matrix is a matrix having the entries above the main diagonal
equal to zero.

5. The n × n identity matrix, I, is the n × n matrix with ones down the diagonal
and zeros elsewhere .

6. The inverse of a square matrix, A, is the matrix A^-1, if it exists, such that
AA^-1 = A^-1A = I.

7. The transpose of a matrix is .

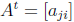8. A symmetric matrix is one that is equal to its transpose.

Discussion

Many matrices have special forms and special properties . Notice that, although
a diagonal matrix must be square, no such condition is put on upper and lower
triangular matrices.

The following matrix is a diagonal matrix (it is also upper and lower triangular ).

The following matrix is upper triangular.

The next matrix is the transpose of the previous matrix . Notice that it is lower
triangular.

The identity matrix is a special matrix that is the multiplicative identity for any
matrix multiplication. Another way to define the identity matrix is the square matrix
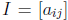where 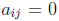if i ≠ j and 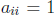. The n × n identity I has the property
that IA = A and AI = A, whenever either is defined. For example,

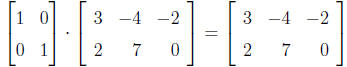
The inverse of a matrix A is a special matrix A^-1 such that AA^-1 = A^-1A = I. A
matrix must be square to define the inverse. Moreover, the inverse of a matrix does
not always exist.

Example 4.4.1.

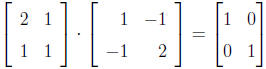
so that

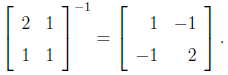
The transpose of a matrix is the matrix obtained by interchanging the rows for
the columns. For example, the transpose of

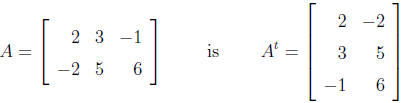
If the transpose is the same as the original matrix, then the matrix is called
symmetric. Notice a matrix must be square in order to be symmetric .

We will show here that matrix multiplication is distributive over matrix addition.

Let and be m × n matrices and let be an n × p
matrix. We use the definitions of addition and matrix multiplication and the distributive
properties of the real numbers to show the distributive property of matrix
multiplication. Let i and j be integers with 1≤ i ≤ m and 1 ≤ j ≤ p. Then the
element in the i-th row and the j-th column in (A + B)C would be given by

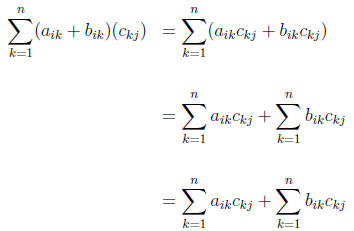
This last part corresponds to the form the element in the i-th row and j-th column
of AC + BC. Thus the element in the i-th row and j-th column of (A + B)C is the
same as the corresponding element of AC + BC. Since i and j were arbitrary this
shows (A + B)C = AC + BC.

The proof that C(A+B) = CA+CB is similar. Notice that we must be careful,
though, of the order of the multiplication. Matrix multiplication is not commutative.

4.5. Boolean Arithmetic . If a and b are binary digits (0 or 1), then

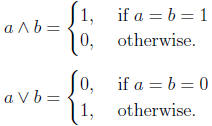
Definitions 4.5.1. Let A and B be n × m matrices.

1. The meet of A and B: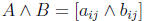
2. The join of A and B: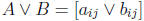

Definition 4.5.1. Let be m × k and be k × n. The Boolean
product of A and B, , is the m × n matrix defined by

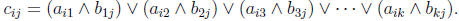
Discussion

Boolean operations on zero -one matrices is completely analogous to the standard
operations, except we use the Boolean operators 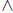and 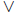on the binary digits instead
of ordinary multiplication and addition , respectively.

4.6. Example 4.6.1.

Example 4.6.1. Let

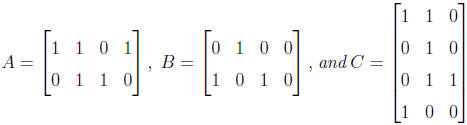
Then

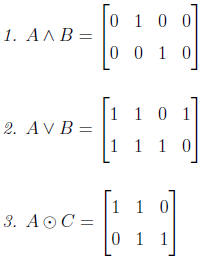
Here are more details of the Boolean product in Example 4.6.1:

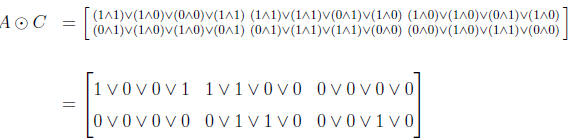
Exercise 4.6.1.

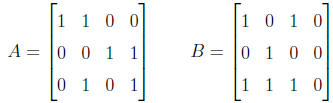
Find

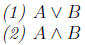
Exercise 4.6.2.

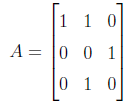
Find

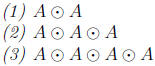
Exercise 4.6.3.

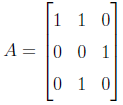
Find 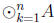, the Boolean product of A with itself n times . Hint: Do exercise 4.6.2
first.