Rational Exponents
• Definition of 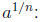 If n is
a positive integer greater than 1 and
If n is
a positive integer greater than 1 and 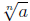 is a
real number , then
is a
real number , then
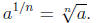
Rewrite as a radical expression and simplify if possible.
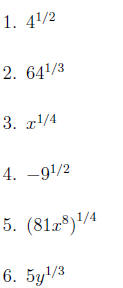
• Definition of 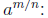 If m
and n are positive integers greater than 1 with
If m
and n are positive integers greater than 1 with
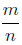 in simplest form , then
in simplest form , then
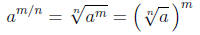
as long as 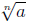 is a real
number .
is a real
number .
Use radical notation to rewrite each expression. Simplify if possible.
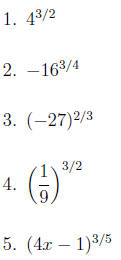
• Definition of 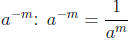 as
long as
as
long as 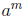 is a nonzero real number.
is a nonzero real number.
Write each expression with a positive exponent. Then simplify.

• Summary of Exponent Rules
If m and n are rational numbers , and a, b, and c are numbers for which the
expressions below exist,
then
Product rule for exponents :
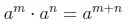
Power rule for exponents:
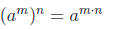
Power rules for products and quotients :
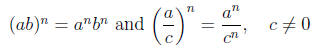
Quotient rule for exponents :
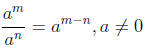
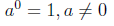
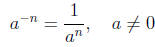
Use the properties of exponents to simplify .
| Prev | Next |