Lesson Plan Outline for I²T² Project

“Factoring Trinomials Station Activity”
Grade Level: 8^th
Course: Algebra
Time: Approximately 40 minutes (1 class period)
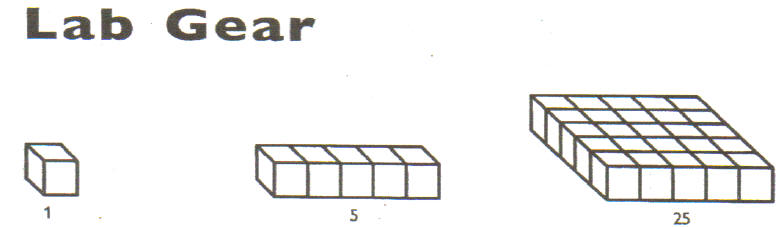
Technology/Manipulatives Used: Algebra Tiles or Lab Gear Algebra Blocks
Submitted by:
Melanie R. Grabek

Table of Contents

1. Lesson Outline Page 1
2. Picture of Lab Gear Page 4
3. Activity Worksheet :Factoring Trinomials Page 5
4. Personal Video Tape Release Form Page 7
5. Student Video Tape Release Form Page 8

Lesson Plan Outline

Title: Factoring Trinomials Station Activity
Grade Level: 8^th
Materials:
• Algebra Blocks or Algebra Tiles
• Corner Piece
• 3x5 cards
New York State
Learning Standards:

• Problem Solving Strand :
8.PS.9 Work backwards from a solution
8.PS.11 Work in collaboration with others to solve problems
• Communication Strand:
8.CM.4 Share organized mathematical ideas through the manipulation of objects, numerical tables,
drawings, pictures, charts, graphs , tables, diagrams, models and symbols in written and
verbal form
• Connections Strand:
8.CN.1 Understand and make connections among multiple representations of the same
mathematical idea
• Representation Strand:
8.R.1 Use physical objects, drawings, charts, tables, graphs, symbols, equations , or objects
created using technology as representations
8.R.6 Use representations to explore problem situations
8.R.8 Use representation as a tool for exploring and understanding mathematical ideas
• Algebra Strand:
8.A.5 Use physical models to perform operations with polynomials
8.A.8 Multiply a binomial by a monomial or a binomial ( integer coefficients )
8.A.11 Factor a trinomial in the form ax^2 + bx + c; a=1 and c having no more than three sets of
factors

Objectives:

Upon completion of this lesson, students will:

• Be able to factor trinomials using Lab Gear Algebra Blocks (See attached
sheet with picture of blocks) or Algebra Tiles.
• Visualize factoring through use of algebra blocks/tiles and the area model.

Developmental Activity:
(See attached worksheet)

Summary:

The students will be working in groups of four . Stations should be set up around the classroom,
each with its own set of algebra blocks/tiles. Each group will be provided with a different 3x^5
card with the multiplication of two binomials displayed on it. (The instructor creates these before
the lesson, with multiplication problems of varying degrees. Start out with a problem such as
(x + 1)(x +1) and then progress to problems such as (3x + 2)(x + 2)). The students will then use
the algebra blocks to perform the operation. Next, the students will remove the blocks
representing the binomial multiplication from their block set-up, and leave the rectangular array
representing the answer to the multiplication problem in the middle. Each group will then proceed
to visit the other groups’ areas, and try to determine what the original multiplication problem had
been, or factor the trinomial. They will be given a time limit at each station, and record the results
of their findings. A worksheet is provided with step by step instructions and tables to record their
data.

Detailed Instructions:

1. Set up stations around the classroom so that groups of 2 – 4 students can work at them.
2. Each station should have a set of Algebra Blocks/Tiles and a corner piece.
3. Each student should be provided with a worksheet (see attached).
4. Prior to the lesson, create a set of 3x5 cards with binomial multiplication problems on them.
Ex. (x + 1)(x + 1), (2x + 1)(x + 1), etc.
5. Explain to students that they will be working in teams to solve puzzles. They will be given a
card with a secret problem on it. It is the job of the other teams to try and figure out what problem
each group had.
6. Pass out the 3x5 cards to each group.
7. Instruct students to perform the indicated problem with their algebra blocks/tiles. The
binomials should be set up on the outside of the corner piece, and the solution should be set up in
the middle so that a rectangular array is formed in which every break line lines up.

Example:

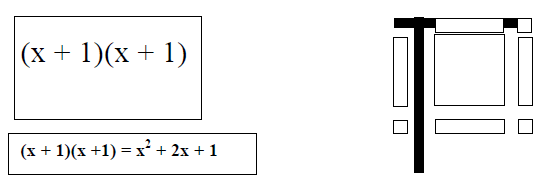
8. Once the students have completed the multiplication problem, they should draw a picture of
their block set up and record their multiplication problem on their worksheet.
9. Next, have the groups take the binomials from the outsides of the corner piece and put them
away, leaving only the blocks in the middle.
10. The groups should then mix up the blocks in the middle so that the next group has to rearrange
it again.
11. Once every group is ready, have the groups move onto the next station. Once there, they
should try to form a rectangular array in the middle, making sure all break lines go through, and
then determine which binomials should go on the outsides of the corner piece.
12. Once finished with step 11, the students should record their results in the table provided on the
worksheet.
13. If you do not have a lot of time to complete this exercise, you can set up a timer so that each
group only gets a set amount of time at each station.
14. After every group is ready, or the timer has sounded, the groups then proceed to the next
station, and repeat the steps discussed until they have completed every station.

Closing:

After the activity is completed, each group will present their original multiplication problem to the
class, and the students will check to see if they were successful in their factoring.

Factoring Trinomials

1. Using the algebra blocks and gray corner piece, multiply the two binomials on the card.

Example:

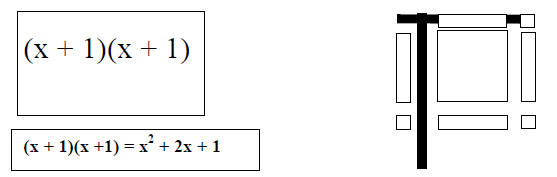
2. Record the expression that is the answer to the multiplication on your card here:

3. Sketch a picture of your set-up on the corner piece
provided here:

4. Next, remove the algebra blocks that represent the two binomials from the outside of the gray
corner piece and put them away.

5. Mix up the blocks that you have left. Once every group has finished, move over to the next table.

6. Once you are at your new table, working as a team rearrange the blocks to form a rectangle that
will fit inside the gray corner piece (remember to check your break lines).

Example:

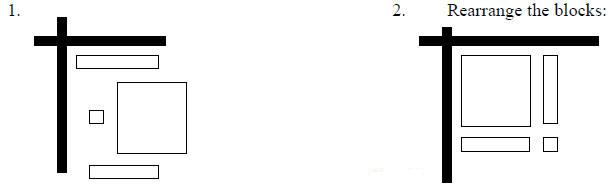
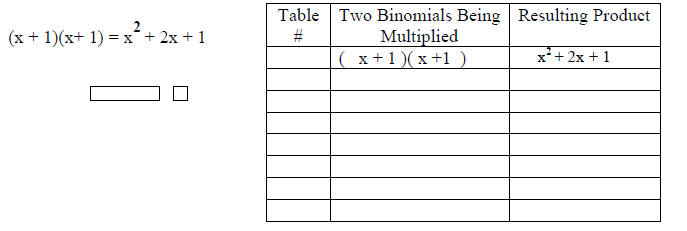
8. Next, figure out what two binomials can be placed on the outside of the corner piece that, when
multiplied, give you the product or rectangle inside the gray corner piece. Record your results in
the table.

Example:

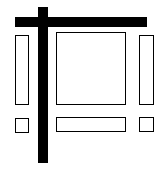
10. Check your answer by multiplying the two binomials together. Does your answer match the
expression in the middle?

11. Continue to do this process until you have visited every groups table and recorded your results.

TABLE OF RESULTS

Table #	Two Binomials Being Multiplied	Resulting Product

VIDEOTAPE RELEASE FORM

Please check the statement that applies.

___ I hereby consent to and authorize the use and reproduction by Buffalo State, or anyone authorized by
the college, of any and all videotapes in which I appear without compensation to me. The videotape shall
constitute the property of the college and may be selected for use to document the knowledge and skills of
teacher education majors for a continuing accreditation review by the National Council for the
Accreditation of Teacher Education.
______________________________ _______________________
Signature Date
______________________________
Name (Please print)

____ I do not consent to or authorize the use or reproduction by Buffalo State of any videotapes in which
I appear.
______________________________ __________________________
Signature Date
______________________________
Name (Please print)

*** Video Permission Forms are on file at Niagara Middle School
Fall Semester, 2004

Dear Parents:

I am currently working on my degree in ______________ Education at Buffalo State
College. As a student teacher in _________'s classroom, it is necessary for me to videotape
_______ lessons as part of my evaluation. The videotape will be used only for evaluation
purposes by my college supervisor and me.
If you choose not to have your child videotaped during class, I can seat or position your
child so that s/he cannot be seen in the video. Please indicate your preference by checking the
statement below that reflects your choice, signing and dating the form, and having your child
return the form to me at school no later than _________________.
Please check one of the following:
_____ I give permission to have my child videotaped.
_____ I give my child permission to be videotaped, providing his/her face
is not filmed.
_____ I do not wish to have my child appear in any video recording.
(S/he will sit out of range of the camera on recording dates)
Parent’s Signature:___________________________
Date:_________________
Student’s Signature:__________________________
Date:_________________
Thank you in advance for your cooperation.
Sincerely,
Student Teacher