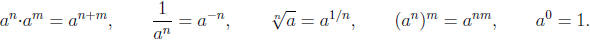Algebra Worksheet
USEFUL FORMULAS:
Arithmetic formulas
(a−b)(a+b) = a2−b2,
(a+b)2 = a2+2ab+b2,
(a−b)2 = a2−2ab+b2.
Rules concerning logarithms
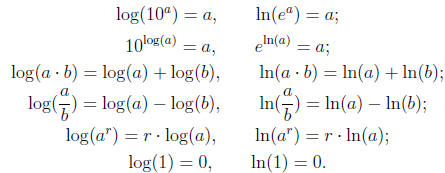
Rules about solving equations
• Whenever you divide by some number make sure it is not 0!
• If a fraction is 0 then this means its numerator is 0, i.e.
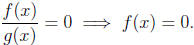
• If a product is equal to 0 than one of its parts is zero, so check
all of them, i.e.
f(x) · g(x) = 0 => solve f(x) = 0 and g(x) = 0.
• Know the quadratic formula and remember that if x2+bx+c
= 0
has roots
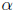 and
and
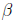 then x2 + bx + c = (x −
then x2 + bx + c = (x −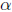 ) · (x −β
).
) · (x −β
).
1. Decide if the following are TRUE or FALSE.
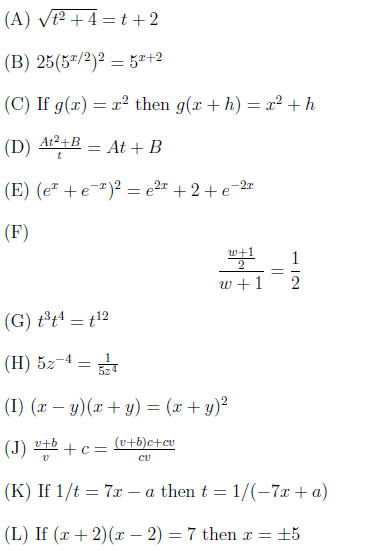
2. Solve for t: (t − 5)(t + 1) = 11
3. Solve for θ:
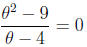
4. Solve for y in terms of x : x2 + 3y = −7xy + 11.
5. Does the following equation determine y as a function
of x: y2 −
x3 = αx.
6. Solve for T and simplify as much as possible:
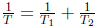
7. The following sequence of exercises is meant to review
basic identities
that you should know.
Start with (x + 2)2 and do the multiplication, you should get x2 +
4x + 4.
Now do the same for (x + 3)2, (2 + x)2 and (x + y)2.
At this point you should see that there is an actual formula that one
can use in for each of these . The formula is
(A + B)2 = A2 + 2AB + B2.
Next, start with (x − 2)2 and do the multiplication, you
should get
x2 − 4x + 4.
Now do the same for (x − 3)2, (2 − x)2 and (x − y)2.
Again you should see that there is a convenient formula
(A − B)2 = A2 − 2AB + B2.
The two formulas above are the basic tools for completing
the square.
There is one more formula that is important. Here is a way to get it.
Multiply (x − 1)(x + 1), what do you get?
Now do the same for (x+2)(x−2), (x−7)(x+7), and (x−y)(x+y).
Do you see a formula?
You always have
(A − B)(A + B) = A2 − B2.
Now that you know the basic formulas let’s do some
exercises with
them. The next exercise aims to do exactly this.
8. Simplify
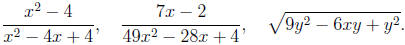
9. Write as a single log
log z 2 + log 10 + log(y − x);
7 log y − 12 logα − 11 log e.
10. Find or simplify the following expressions :
(A)
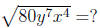
(B) (x − 7)(x + 7) + 49 =?
(C) −(x − 5)2 =?
(D) (3y + 1)(1 − 3y) =?
(E) (y3 − 3)(y3 + 3) =?

11. Factor the following expressions
(A) y(y − 3) + 15(3 − y)
(B) 7x2 + 14x − 21
(C)
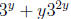
(D) x2 − x − 1
(E) (x − 1)(x + 1) + x2 − 2x + 1.
| Prev | Next |