Factoring_Trinomials32
Factoring Trinomials of the Form x2 + bx + c
Trinomials, such as x2 + 5x + 6 and x2-4x- 21, are called trinomials of the form
x2 + bx + c
because the coefficient " squared " term is 1. In general, x2 is called the first
or leading term, bx
is called the middle term, and c is called the last or constant term. The steps
we use to factor
trinomials of this form are based on the patterns that occur when we FOIL
binomials.
1) Arrange the terms in descending order (from highest power to lowest power) so
that the
expression takes the form: x2 + bx + c .
2) Look for a GCF (Greatest Common Factor) and factor it out first. When the
leading term
is negative , the GCF is "−1." To factor out a gcf of −1, change the sign on each
term.
3) Set up the first terms. Because x2 = x□x , the first term of each binomial
factor is "x:"
(x )(x )
4) Determine the signs of the binomial factors .
When the constant term is positive ,
! Binomial factors have the same sign: (x + )(x + ) or (x − )(x − ).
! The middle term has the same sign as the binomial factors.
! Factors of the constant term add to "b," the coefficient of the middle term.
When the constant term is negative,
! Binomial factors have opposite signs: (x + )(x − ) or (x − )(x + ).
! Factors of the constant term c subtract to "b."
! The larger factor of these factors has the same sign as the middle term.
5) Find factors of "c" that sum to "b" list the factors of the constant term to
find the pair
of factors whose product is "c" and whose sum is "b." (Note: if factors of the
constant
term do not sum to "b," the expression is "prime" and cannot be factored.)
7) Write the factorization using the factors found in step 5.
6) Check the result by multiplying.
Example: Factor 2x + 8 x2
Step 1: The terms of the expression are not in descending order. Rearrange the
terms so
that they take the form x2 + bx + c.
2x + 8 − x2 = −x2 + 2x + 8
Step 2: Look for a GCF because the leading term is negative, the GCF is −1.
Factoring out
the GCF gives us:
−x2 + 2x + 8 = −(x2 − 2x − 8)
Step 3: Next, factor the inside expression x2 − 2x − 8 . Because x2 = x x, the
first term of
each binomial factor is "x:"
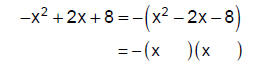
Step 4: Determine the signs of the binomial factors. The constant term is
negative. This
means the binomial factors have opposite signs:
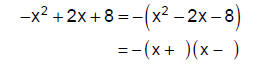
Step 5: Find the factors of 8 that sum to 2, the
coefficient of the middle term. Because the
middle term is negative, the larger factor of 8 must be negative. Factors of 8
that sum to
2 are 2 and 4.

Step 6: Write the factorization using the factors found in Step 5. Don’t forget
to write the GCF
as part of the factorization!
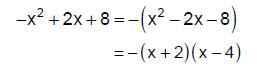
Step 7: To check the result, multiply the binomial factors first then distribute
the GCF:
−(x + 2)(x − 4) = −(x2 − 4x + 2x − 8) = −(x2 − 2x − 8) = −x2 + 2x + 8
| Prev | Next |