Generating Functions
1 Algebra and Infinity
2 Generating Functions
3 Recurrences
4 Regular Languages and Generating Functions
Finite versus Infinite
Finite state machines are a great example of a finite, algorithmically
attractive
representation of an infinite object (the acceptance language or, in case of
infinite words, even just a single accepted word).
Register machines and Turing machines also describe infinite objects, but
they
are much less amenable to manipulation by algorithms.
Are there any other compelling examples along the lines of finite state
machines? How about something more algebraic?
Classical Example: Making Change
Suppose we have an unlimited supply of coins of denominations
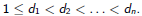
How many ways are there to make change for x ≥0?
Call this number C (x).
In other words, we want to count the number of solutions of the equation
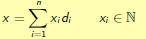
The standard approach to computing C(x) is dynamic programming.
Counting
More precisely , in the bottom-up approach we compute a n × (x + 1) array
C(k, z) where 1≤k≤n and 0≤z≤x
with the intent that
C(k, z) = # of ways to make change for z using d1, . . . , dk
Then
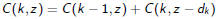
where C(k, 0) = 1 and C(k, y) = 0 whenever y < 0 or k = 0.
So we can get C(z), z≤x, in
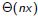steps.
Example
The table for d = (2, 5, 10) and x = 18.
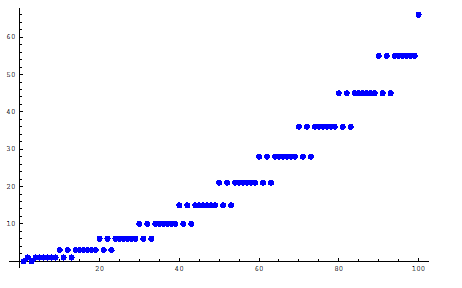
Computing a few more values produces the following plot. Ponder deeply.
C(x) for x≤100, d = (2, 5, 10).
Expanding Polynomials
Another way to get numerical answers is to multiply together polynomials
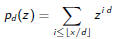
for d = d1, . . . , dn.
Claim
The coefficient of
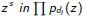is
C(s), for all s≤x.
This follows immediately from the definition of polynomial multiplication .
Notation
We write
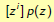
for the coefficient of term zi in the polynomial p(z).
So
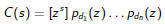
for all s≤x.
Going Infinite
The bound s≤x is annoying. It would be nice to be able
to deal with the
whole infinite sequence
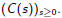
We would like to set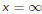 
in
the definition of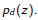 
That’s actually OK, except that we are now dealing with a power series instead
of a polynomial.
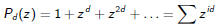
Then
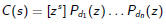
for all s≥0.
The Crucial Trick
So far, we have not really gained much: to compute the coefficients of the
product power series we have to multiply out polynomial of sufficiently high
degrees, just as before.
But note that
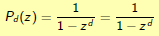
Instead of using infinitary power series we can use perfectly finitary
rational
functions!
Example (2,5,10)
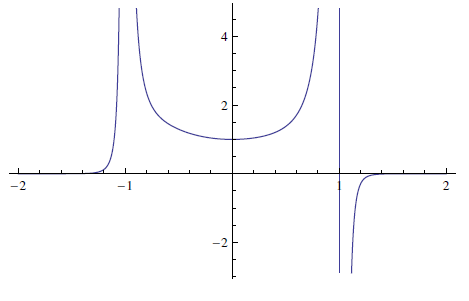
Taylor Expansion
There is price we have to pay, though: given a rational function , it becomes
a
bit more difficult to extract the coefficients of the corresponding power
series.
For example, expansion about z = 0 produces
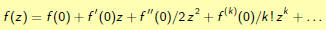
Evaluating the derivatives requires quite a bit of work.
Getting a nice closed form can be very hard.
Example
The rational function looks like
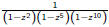and C(s) has the form
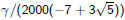where γ is this:
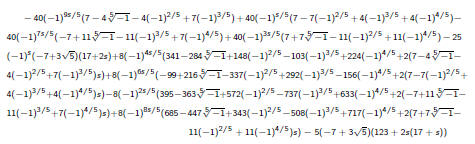
It is not even clear that this simplifies to a integer value (it does, for
all s≥0).
The best way to check is by machine.
Algebra and Infinity
2 Generating Functions
Recurrences
Regular Languages and Generating Functions
The Definition
Suppose we have a sequence
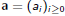of numbers (naturals, integers, reals,
whatever).
Definition
The generating function of a is the power series
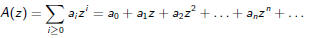
Note that z is just a variable and could be replaced by any other variable.
At first glance, A(z) may look slightly more complicated than a, so why bother?
Aside: The Calculus Angle
We will mostly ignore issues of convergence here, we are not really
interested in
evaluating the series A(z).
Still, note that for “reasonable”
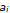and sufficiently small z we will
actually get a
function from, say, the reals to the reals.
Lemma
Let r > 0 such that
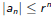for all n > 0. Then A(z) converges for all z such
that |z| < 1/r .
One can use the machinery of analysis to determine properties of this
function
and, hopefully, get a better understanding of a.
In particular, one can use Taylor expansion to retrieve the
coefficients given
some suitable representation of the series, more later.
Algebra
The real goal is to the algebra of power series–rather than manipulating the
sequence directly, we manipulate the series. For example,
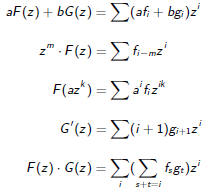
Manipulating Infinite Sequences
So we can perform certain operations on sequences:
• Add two sequences .
•Multiply a sequence by a scalar.
•Multiply a sequence by 1,2,3,. . .
•Shift a sequence to the right or left.
•Space out a sequence.
•Convolve two sequences.
Given a few basic sequences this allows us to construct a whole class of
sequences.
Standard Generating Functions
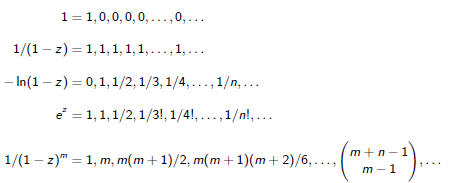
Roll Your Own
How do we concoct the generating function for
1, 1, 2, 2, 4, 4, 8, 8, . . .
No problem:
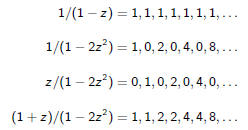
The Inevitable Urn Example
You have an urn containing 30 red, 40 blue and 50 white balls. How many
ways are there to extract 70 balls from the urn (order does not matter)?
Letting
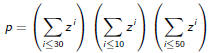
we need to calculate [z70] p.
We could expand out the whole polynomial, but a better way is to rewrite the
geometric sums as
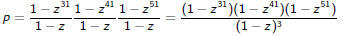
Urn
The denominator term 1/(1 − z)^3 can be expanded according to the binomial
theorem as
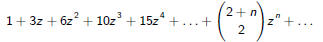
Since we are looking for z70 we only need the part
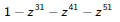
from the numerator , all other terms have higher degree. So the answer is
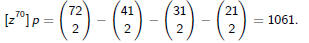
Sicherman Dice
A pair of standard dice produce the following relative frequencies for the 11
possible outcomes:
Weird Question: Can we get the same frequencies using non-standard
dice?
Let’s agree that the dice have 6 faces and the number of spots on each face is
positive.
A priori there are 12 variables to deal with, one for each face. Of course,
there
are constraints that simplify matters, but it’s still a bit tedious to try out
“random” spot assignments.
George Sicherman seems to be the first to have solved this problem
The High Road
We can describe an ordinary die as
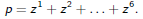
So we would like to find positive exponents ai and bi such that
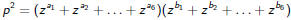
Better is to factor p:
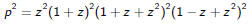
Then the two new polynomials must factor as
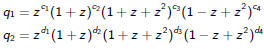
where
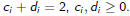
Pinning Down the Coefficients
First note that we must have c1 = d1 = 1 since qi(0) = 0: each face must have
a positive number of spots.
We must have c2 = d2 = c3 = d3 = 1 since qi(1) = 6: there are six faces.
This leaves c4 and d4.
One possibility is, of course, c4 = d4 = 1 and we have
ordinary dice. The only
other possibility is, say, c4 = 0 and d4 = 2 producing two
dice
(1, 2, 2, 3, 3, 4) (1, 3, 4, 5, 6, 8)
That’s it, there are no other solutions.
Algebra and Infinity
Generating Functions
3 Recurrences
Regular Languages and Generating Functions
Recurrences
Generating functions suggest the following general approach towards solving
recurrences:
•Write the solution
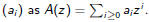
•Apply the recurrence to the terms of the power series and massage things
into a nice closed form.
•Extract the terms of the sequence from the closed form of A(z), e.g., by
Taylor expansion.
Fibonacci
The recurrence here has the form
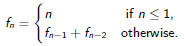
Hence we have the generating function
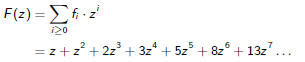
By applying the recurrence to the series we get
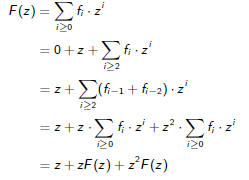
and therefore
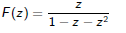
Solution
Since F(z) is a simple rational function, we can determine the coefficients
of
the Taylor series easily using a partial fraction decomposition.
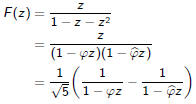
Here
Since
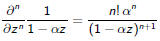
we have
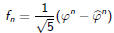
Binary Trees
Let
be the number of (ordered) binary trees on n nodes (which is the
same as
the number of full binary trees on n + 1 leaves).
Brute force table:
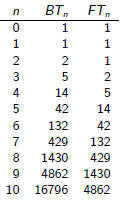
Recurrence
The recurrence for binary trees takes the form
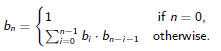
Let B(z) be the generating function and note that
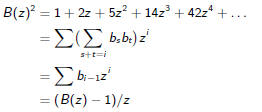
Therefore
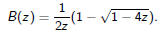
Taylor
Performing Taylor expansion is somewhat difficult in this case, though of
course
not a problem for a computer algebra system:
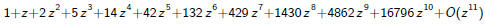
It turns out to be easier to use the Binomial Theorem to get a better
description.
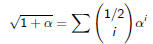
and thus
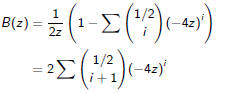
Taylor
A simple calculation shows
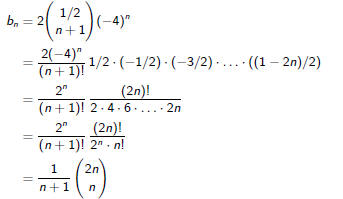
Hence, bn = Cn, the nth Catalan number.
Algebra and Infinity
Generating Functions
Recurrences
4 Regular Languages and Generating Functions
Growth Functions
Recall a definition from a few weeks back:
Definition
Given a language
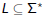its growth function is defined by
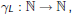
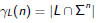
For regular languages growth functions are particularly simple: they have
rational generating functions.
How does one compute
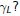
Full Transition Matrices
Suppose we have a DFA M on states [n] that accepts L. Define the full
transition matrix of M to be
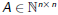where
A(i , j) = # transitions from i to j
Let
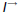be the row unit vector with a 1 at the initial state.
Let
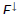be the column vector with 1’s at the final states, 0’s elsewhere.
Claim
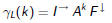
Note that this does not work for nondeterministic machines.
Example: Even/Even
The full matrix for the even/even DFA looks like so:
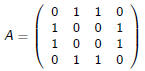
In this case it is easy to calculate Ak :
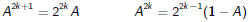
Hence
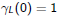and for k > 0 we have
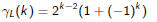
And Generating Functions?
It would seem natural to try to determine the generating function for
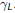
How about something like
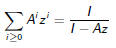
Looks great, but A is a matrix, not a real; the fraction on the right hand
side
requires a bit of explanation (and might just be meaningless).
I is the identity matrix, I − Az is a matrix of linear polynomials in z. Such
a
matrix may well have an inverse, so we should interpret the fraction as a matrix
inverse.
Example: Even/Even
The inverse of (I − Az) for the even/even DFA looks like so:
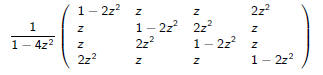
Since q0 = 1 and F = {1} we only need the first term. Taylor expansion
produces
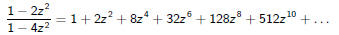
Works! But why?
An Explanation of Sorts
To do this real justice one has to take a closer look at the algebraic
structure of
all formal power series whose coefficients are n × n integer matrices (which is
often written
and has lots of interesting properties).
Less formally, we want to justify
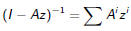
Multiplying both side this simply means:
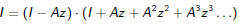
The last equation is easily verified; just multiply out the RHS.
Incidentally, in this formal power series structure there is a Kleene star:
,
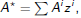the unique solution of X = AX + I .
General Case
Write
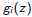for the generating function counting the words that lead from q0 to
i . Let
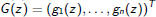be
the column vector of all these functions.
Then we need to solve the linear system
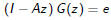
where e is the unit column vector indicating the initial state.
The generating function for
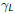is then
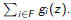
Note that this type of computation can be handled easily on a computer
algebra system; it’s a bit unpleasant to do by hand.
Example: Subword Counter
Recall the problem of building a DFA for all words over {a, b} that contain
exactly three occurrences of the subword ab (subword, not factor).
The state complexity of this language is 7 and the matrix I − Az for the
minimal DFA has the form
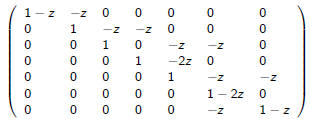
1 is the initial state, 6 is a sink and 7 is final.
Solution
The generating function for
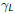is
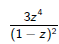
A little bit of pattern matching produces
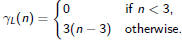
Not exactly earth shattering, but very elegant.
Summary
•Generating functions are another example of a compact description of an
infinite object.
•Combinatorial operations on sequences correspond to algebraic operations
on the corresponding functions.
•Generating functions can be used to solve recurrence equations.
•There is a deep connection between rational generating functions and
regular languages; in particular growth functions of regular languages are
rational.
| Prev | Next |