Math 1113 Final Exam Review
Rouhani
This review should only be used as a guide for preparation
for the final exam. In
addition you should study your notes, homework, and quizzes.
Section 1
Suppose graph of f is given . Describe the following graphs
relative to graph of f
(#1-3).
1.
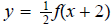
ans: Vertical shrink by a factor of 1/2 units, then horizontal shift of 2
units to the
left
2.
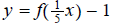
ans: Horizontal stretch of 5 units, then vertical shift of one unit down.
3.
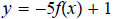
ans: Vertical stretch of 5 units, reflection along x-axis, then vertical
shift of one
unit up.
4. Identify each translation from the function
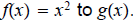 .
.
a.
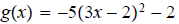
ans: Horizontal shrink by a factor of 1/3, horizontal shift of 2 units to
the right,
vertical stretch by a factor of 5 units , reflection along the x-axis, finally
vertical
translation of 2 units down.
b.
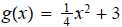
ans: Vertical shrink by a factor of 1/4, then vertical shift of 3 units
up.
c.
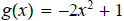
ans; Vertical stretch of 2 units, reflection along x-axis, then vertical
translation
of 1 unit up.
Find the domain of each function.
5.
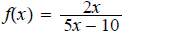 ans:
ans: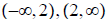
6.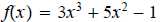 ans:
ans:
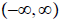
7.
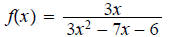 ans:
ans:
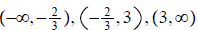
Evaluate the indicated functions, where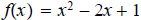 and
and
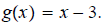
8.
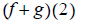 ans: 0
ans: 0
9.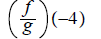 ans: − 25/7
ans: − 25/7
Find f ◦ g for the given functions f and g.
10.
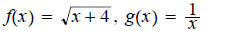 ans:
ans:
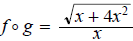
11.
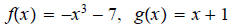 ans:
ans:
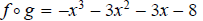
Find inverse of each function.
12.
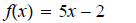 ans:
ans:
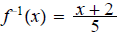
13.
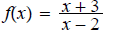 ans:
ans:
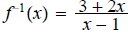
14. Given 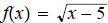 and
and
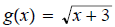 find
find
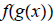 then determine
then determine
domain of f ◦ g.
ans: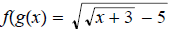 Domain
Domain
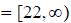
15. Given
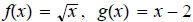 find
find
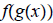 then determine domain of f ◦ g.
then determine domain of f ◦ g.
ans:
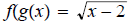 Domain
Domain
Also you should know how to:
a. Identify intervals that a given function is constant,
increasing, or decreasing.
c. Identify the domain and range of a graph of a function.
d. Find inverse of a function given its graph.
e. Use the horizontal and vertical line tests .
f. Find equation of a function given its graph.
g. Distinguish between vertical and horizontal stretch and shrink.
Section 2
1. Find the intercepts of the graph of each function.
a.
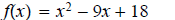 ans: x-intercept:
ans: x-intercept:
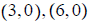 y-intercept:
y-intercept: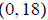
b.
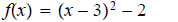 ans: x-intercept:
ans: x-intercept:
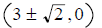 y-intercept:
y-intercept: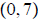
2. Identify any vertical and horizontal asymptotes of the following functions.
a.
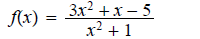 ans: vertical asymptote: none ; horizontal
ans: vertical asymptote: none ; horizontal
asymptote: y = 3
b.
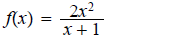 ans :vertical asymptote: x = −1 ; horizontal
ans :vertical asymptote: x = −1 ; horizontal
asymptote: none
c.
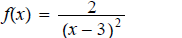 ans: vertical asymptote: x = 3 ; horizontal
ans: vertical asymptote: x = 3 ; horizontal
asymptote: y = 0
3. Find intercepts of each rational function .
a.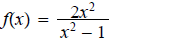 ans: x-int = 0, y-int = 0
ans: x-int = 0, y-int = 0
b.
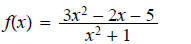 ans: x-int = −1, 5/3 ; y-int = −5
ans: x-int = −1, 5/3 ; y-int = −5
Also you should know:
a. The difference between rational and polynomial
functions .
b. What are zeros of a polynomial functions, and how to find them. How to find
multiplicity of a zero .
c. Even and odd functions
e. How to find average rate of change of functions between two given points.
Section 3
Solve for x (# 1-8).
1.
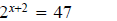 ans:x
≈ 3.55
ans:x
≈ 3.55
2.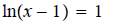 ans:x = 3.71
ans:x = 3.71
3.
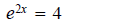 ans:x
≈ 0.69
ans:x
≈ 0.69
4.
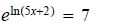 ans: x = 1
ans: x = 1
5.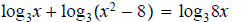 ans: x = 4
ans: x = 4
6.
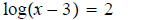 ans:
x = 103
ans:
x = 103
7.
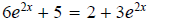 ans: No solution
ans: No solution
8.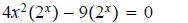 ans:
ans: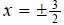
Write the expression as a logarithm of a single quantity.
9.
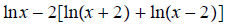 ans:
ans: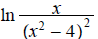
10.
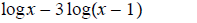 ans:
ans: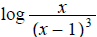
11. Find domain of
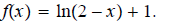 ans:
ans:
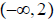
12. Find domain of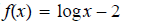 ans:
ans: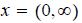
13. Find domain of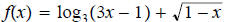 ans:
ans:
Use your graphing utility to sketch the graph of each
function, then state the
domain, range, intercepts and asymptote of f.
14.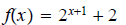
ans: Domain:
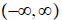 ; Range:
; Range:
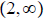 ; x-int: none ; y-int:
; x-int: none ; y-int:
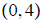 ; asymptote:
; asymptote:
y = 2
15.
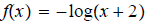
ans: Domain:
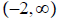 ; Range:
; Range:
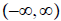 ; x-int:
; x-int: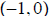 ; y-int:
; y-int: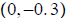 ; asymptote:
; asymptote:
x = −2
16. How long will it take for $2500 to triple if it is
invested in a savings
account that pays 4.5% interest compounded continuously ?
ans: approx 24 years
17. Suppose $3000 is invested into an account paying 6%
interest
compounded quarterly. Find the balance in the account after 5 years.
ans: $4040.56
18. The population of a town is modeled by
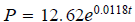 where t = 0
where t = 0
represents the year 2000. According to this model, when will the population
reach 18,000?
ans: year 2615
19. Radioactive stronium decays according to the function
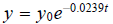 ,
,
where t is time in years.
a. If an initial sample contains y0 = 5 grams of
radioactive stronium, how many
grams will be present after 60 years ?
b. What is the half-life of radioactive stronium?
ans: a. 1.19 grams b. 29 years
20. The half-life of a certain radioactive material is
1200 years.
a. Find the decay constant k. ans: −0.000577
b. What percent of material will remain after 135 years. ans: 92%
| Prev | Next |