Math Choice Questions
Section 11.5
Level: Easy
In the statement of
the Ratio test
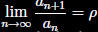 we
we
conclude the series
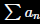 converges if
converges if
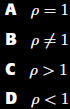
Which of the
following is equal
to (n + 1)!
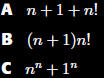
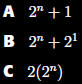
Section 11.6
Level: Easy
We can rearrange
terms in a series
which does not
converge absolutely
so that the value of
the series equals
two different
values.
A True
B False
The series
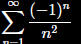
converges
absolutely
A True
B False
The series
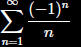
converges
A True
B False
Section N4
Level: Easy
To compute the
interval of
convergence for a
power series you
use
A Integral Test
B Ratio Test
C Comparison Test
D Root Test
To express
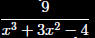 as a
as a
power series our
first step is
A Differentiate
B Integrate
C Partial fractions
To express
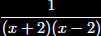 as a
as a
power series our
first step is
A Integrate
B Partial Fractions
C Differentiate
Which of the
following is not a
power series?
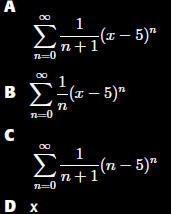
To express ln(1 + x)
as a power series
our first step is
A Partial fractions
B Integrate
C Differentiate
To express atan(x)
as a power series
our first step is
A Partial fractions
B Integrate
C Differentiate
To express x
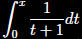 as a
as a
power series our
first step is
A Partial fractions
B Integrate
C Differentiate
To express 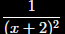
as a power series
our first step is
A Partial fractions
B Integrate
C Differentiate
Section 11.8
Level: Easy
If 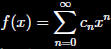
what is f(0)
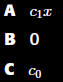
The Taylor series for
f(x) centered at x=0
is 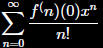
A True
B False
Section 11.8
Level: Hard
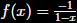 then
then
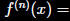
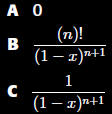
What is the
coefficient of ![]() in
in
the Taylor series for
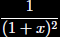 about a=0
about a=0
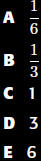
Section 11.8
Level: Easy
A function f has the
following Taylor
series about a = 0
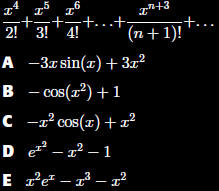
Section 11.8
Level: Hard
Let
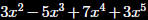
be the fifth-degree
Taylor polynomial
for the function f
about a=0. What is
the value of 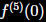

Section 11.8
Level: Easy
The interval of
convergence for
sin(x) is
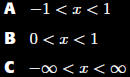
The interval of
convergence for
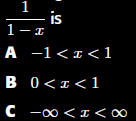
Section 11.9
Level: Easy
What is the power
series for sin(3x)
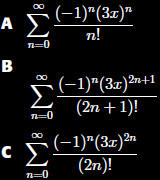
What is the power
series for 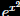
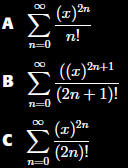
Section 11.9
Level: Hard
What is the power
series for sin(x) - x
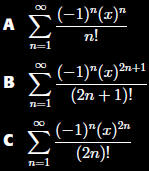
Section 11.9
Level: Easy
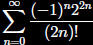 is a
is a
power series for
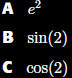
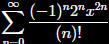 is a
is a
power series for
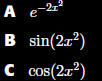
If lf'(t)l < 1,
lf''(t)l < 2 and
lf'''(t)l < 3 for t
with lt - 1l < 2 give
the bound on
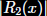 on the
on the
interval [-1, 3]

Section 11.9
Level: Hard
Which function is
larger for small x
(x < 1) by looking
at the first few
terms of their Taylor
Series
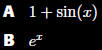
Which function is
larger for small x
(x < 1) by looking
at the first few
terms of their Taylor
Series
| Prev | Next |
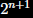 to
to