Math Homework
10pts
1W.
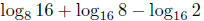
9pts
2W. A 5 ft basketball player stands 20 ft away from the basket. The trajectory
of the ball
that he shoots can be modeled by
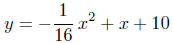
where the basketball ring is located at x = 0 and the
shooter is at x = 20.
Note: The shot was a clean shot, also know as "swish." (In other words, the
trajectory
is not affected by the ring.)
a) What is the height of the basketball ring?
b) What is the maximum height of the ball?
8pts
3W. x4 - 5x3 + 3x2 + 19x - 30
Compute all zeros knowing that 2 + i is one of them.
12pts
4W. x4 + 2x3 - 9x2 - 2x + 8
a) State all possible rational zeros .
b) Find all rational zeros using synthetic division .
c) Find all irrational zeros if any.
15pts
5M. Choose one of these and solve for x :
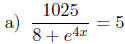
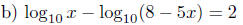
25pts
6M. Match the graph to the equation :
a) Exponential growth model y = aebx, b > 0
b) Exponential decay model y = ae-bx, b < 0
c) Gaussian model
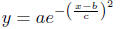
d) Logistic growth model
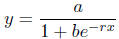
e) Logarithmic model y = a + b ln x

10pts
7M. $7550 is deposited in an account that pays 7.25% interest compounded
continuously .
How many years will it take for the money to triple? (Leave ln in your answer.)
8M. (Example 5 in Section 3.5)
On a college campus of 5000 students, one returns from vacation with a
contagious
and long lasting flu virus. The spread of the virus is modeled by
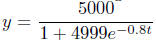
where y is the total number of students infected after t days. The college will
cancel
classes when 40% or more of the 5000 students are infected.
5pts a) How many students are infected after 5 days? (Set up equation , do not
solve.)
5pts b) After how many days will the college cancel classes? (Leave ln in your answer.)
Bonus Problem: 10 points
1. Find x intercepts by setting y = 0 and solving.
2. Find y intercepts by setting x = 0 and solving.
3. Find vertical asymptotes by setting denominator = 0 and solving.
4. Find horizontal asymptotes by comparing highest powers in numerator and
denomi -
nator.
5. Draw a factor picture to see when the graph is above the x-axis and when it
is below
the x-axis.
6. Draw arrows next to the asymptotes on the basis of #5 results.
7. Graph function by connecting the dots.
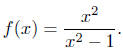
| Prev | Next |