Math Problems Set 8
Discussion: Oct. 25, Oct. 27 (on polynomials and floor
functions) The name after
the problem is the designated writer of the solution of that problem . (Beth,
Nicholas, and
Frank are exempted this week)
Discussion Problems
1. (a) Factor the polynomial x8 +98x4 +1 into two factors with integer (not
necessarily
real) coefficients.
(b) Find the remainder on dividing x 100 - 2x51 + 1 by x2
- 1. (Shelley)
(Hint: (a) 98 = 100 - 2; (b) Bezout’s theorem)
2. If 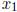 and
and 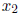 are the zeros of the polynomial x2
- 6x + 1, then for every
nonnegative
are the zeros of the polynomial x2
- 6x + 1, then for every
nonnegative
integer n, 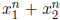 is an integer and not divisible by 5. (Derek) (Hint: how about
is an integer and not divisible by 5. (Derek) (Hint: how about
induction?)
3. (VA 1982) Let p(x) be a polynomial of the form p(x) = ax2 + bx + c, where a,
b and
c are integers, with the property that 1 < p(1) < p(p(1)) < p(p(p(1))). Show
that
a ≥ 0. (Brett) (Hint: by contradiction)
4. (VA 1987) A sequence of polynomials is given by
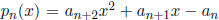 ,
for
,
for
n ≥ 0, where 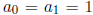 and, for n ≥ 0,
and, for n ≥ 0,
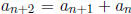 . Denote by
. Denote by
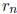 and
and 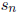
the roots of 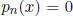 , with
, with
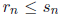 . Find
. Find 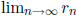 and
and 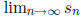 . (Ben) (Hint:
. (Ben) (Hint:
think about 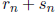 and
and
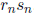 .)
.)
5. (VA 1991) Prove that if α is a real root of (1-x2)(1+x+x2+· · ·+xn)-x = 0 which
lies
in (0, 1), with n = 1, 2, · · · , then is also a root of
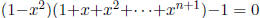 .
.
(Lei) (Hint: use 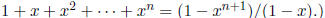
6. (VA 1996) Let ![]() , i = 1, 2, 3, 4, be real numbers such that
, i = 1, 2, 3, 4, be real numbers such that
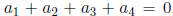 .
.
Show that for arbitrary real numbers 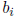 , i = 1,
2, 3, the equation
, i = 1,
2, 3, the equation 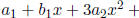
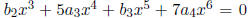 has at least one real root which is on the
interval
has at least one real root which is on the
interval
-1 ≤ x ≤1. (Tina) (Hint: think integral)
7. (VA 1995) Let
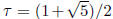 . Show that
. Show that
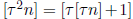 for every positive integer
for every positive integer
n. Here [r] denotes the largest integer that is not larger than r. (David Rose)
(Hint:
prove ≥ and ≤ both hold.)
8. Solve the equation z 8 + 4z6 - 10z4 + 4z2 + 1 = 0. (Lei) (Hint: divide it by
z4, and
observe the symmetry)
9. (Putnam 2004-B1) Let
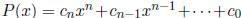 be a polynomial with
integer
be a polynomial with
integer
coefficients. Suppose that r is a rational number such that P(r) = 0. Show that
the
n numbers
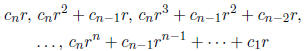
are integers. (Davis Edmonson)
10. (Putnam 2003-B1) Do there exist polynomials a(x),
b(x), c(y), d(y) such that
1 + xy + x2y2 = a(x)c(y) + b(x)d(y)
holds identically? (Richard)
More Problems:
1. If a and b are two solutions of x4 -x3 -1 = 0, then ab is a solution of x6
+x4 +x3 -
x2 - 1 = 0.
2. Suppose that a, b, c are distinctive integers. Prove
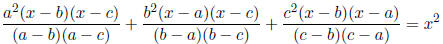
for any x ∈ R.
3. (VA 1997) Suppose that 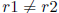 and
and
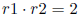 . If
. If 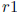 and
and
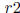 are roots of x4
- x3 +
are roots of x4
- x3 +
ax2 - 8x - 8 = 0, find 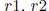 and a. (Do not assume that they are real numbers.)
and a. (Do not assume that they are real numbers.)
4. (VA 1991) Let f(x) = x5 - 5x3 + 4x. In each part (i)–(iv), prove or disprove
that
there exists a real number c for which f(x) - c = 0 has a root of multiplicity
(i) one,
(ii) two, (iii) three, (iv) four.
5. (VA 1985) Let 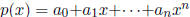 , where the coefficients
, where the coefficients
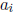 are real.
Prove that
are real.
Prove that
p(x) = 0 has at least one root in the interval 0 ≤ x ≤1 if
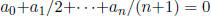 .
.
6. (VA 1989) Let a,b, c,d be distinct integers such that the equation (x - a)(x
- b)(x -
c)(x-d)-9 = 0 has an integer root r. Show that 4r = a+b+c+d. (This is
essentially
a problem from the 1947 Putnam examination.)
7. (VA 1988) Find positive real numbers a and b such that f(x) = ax - bx3 has
four
extrema on [-1, 1], at each of which |f(x)| = 1.
8. (VA 1987) Let p(x) be given by 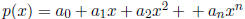 and let |p(x)|
≤ |x|
and let |p(x)|
≤ |x|
on [-1, 1]. (a) Evaluate 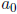 . (b) Prove that
. (b) Prove that
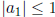 .
.
9. (VA 1990) Suppose that P(x) is a polynomial of degree 3 with integer
coefficients and
that P (1) = 0, P(2) = 0. Prove that at least one of its four coefficients is
equal to or
less than -2.
10. (Putnam 2004-A4) Show that for any positive integer n, there is an integer N
such
that the product 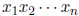 can be expressed identically in the form
can be expressed identically in the form
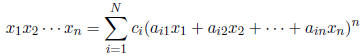
where the 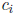 are rational numbers and each
are rational numbers and each
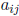 is one of
the numbers -1, 0, 1.
is one of
the numbers -1, 0, 1.
11. (Putnam 2003-A4) Suppose that a, b, c, A,B,C are real
numbers, a ≠ 0 and A ≠ 0,
such that
|ax2 + bx + c| ≤ |Ax2 + Bx + C|
for all real numbers x. Show that
|b2 - 4ac| ≤ |B2 - 4AC|.
12. (Putnam 2003-B1) Do there exist polynomials a(x), b(x), c(y), d(y) such that
1 + xy + x2y2 = a(x)c(y) + b(x)d(y)
holds identically?
13. (Putnam 2003-B4) Let
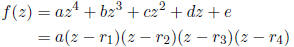
where a, b, c, d, e are integers, a ≠ 0. Show that if
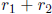 is a rational
number and
is a rational
number and
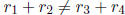 , then
, then 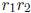 is a rational number.
is a rational number.
| Prev | Next |