Multiplying and Simplifying Rational Expressions
Multiplying and Simplifying Rational Expressions
A. Rational Expressions and Replacements
* A rational expression is an expression that can be
written in the form P/Q ; where P
and Q are polynomials .
Ex. Find the numerical value of
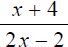 when x=3.
when x=3.
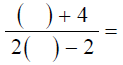
* Because rational expressions indicate division , we must
be careful to avoid
denominators of zero . When a variable is replaced with a number that produces a
denominator equal to zero, the rational expression is not defined.
Ex. Find all numbers for which the given rational expression is not defined.
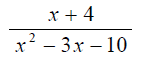
*Note* The value of the numerator has no bearing on
whether or not a rational expression is
defined. To determine which numbers make
the rational expression not defined, we set
the denominator equal to 0 and solve .
B. Multiplying by 1
* We multiply rational expressions in the same way that we
multiply fraction notation in
arithmetic .
Multiplying Rational Expressions: To multiply
rational expressions, multiply
numerators and multiply denominators.
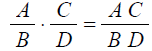
For example,
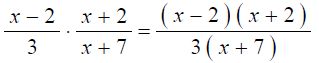
* Any rational expression with the same numerator and denominator is a symbol for 1.
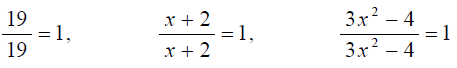
Ex.
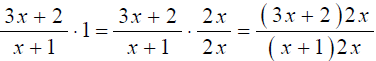
Ex.
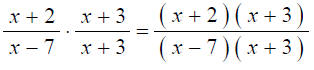
Ex.
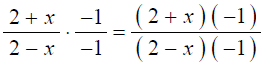
C. Simplifying Rational Expressions
Ex. Simplify each rational expression. ( by factoring and reducing )
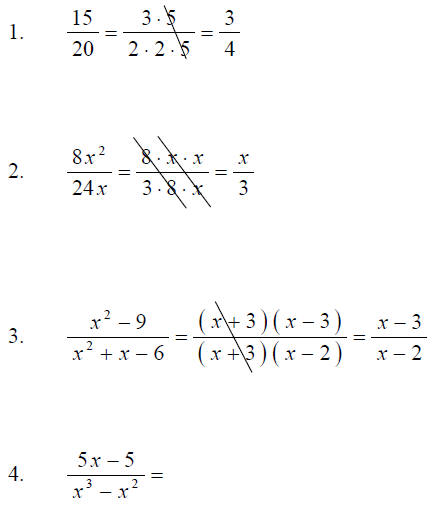
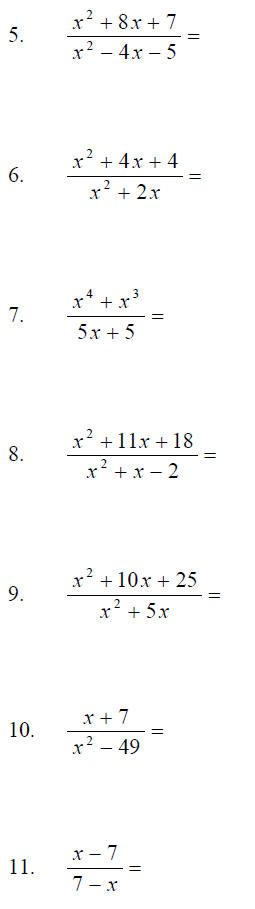
D. Multiplying and Simplifying
Ex. Multiply and simplify.
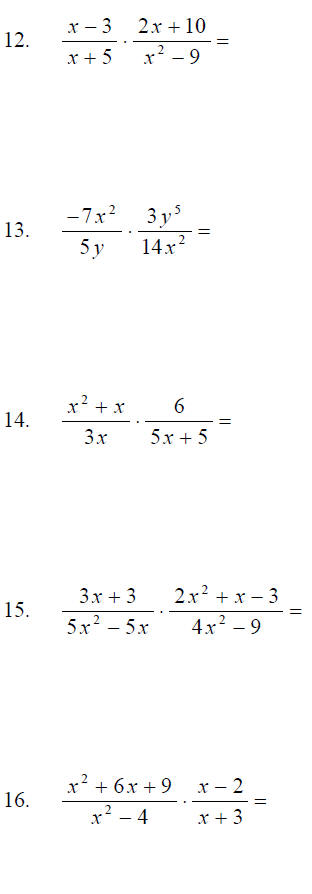
| Prev | Next |