Prime Numbers and GCF
Definitions:
•Prime number – A natural number other than 1 that has
exactly two different factors, 1 and the number itself
o 2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, …...
•Composite number – A natural number that has factors
other than 1 and itself
o 4, 6, 8, 9, 10, 12, 14, 15, 16, 18, 20, ……
•Prime factorization – A number written as a product of only prime numbers
•Greatest common factor – The largest number that divides all given numbers with no remainder
Objective 1: Determine is a number is prime, composite or neither
•There are shortcuts in determining if a number is
divisible by another number:
o Even #’s are all divisible by “2”
o To determine if a # is divisible by “3”, add the digits up and if the answer
is equal to a number divisible by “3”, then so is the #.
Example:
| 12 | 108 | 1284 |
| 1 + 2 = 3 | 1 + 0 + 8 = 9 | 1 + 2 + 8 + 4 = 15 |
o Anything ending in a “0” or a “5” is divisible by “5”
o To determine if a number is divisible by “9”, follow the same rules as you did
for the # 3, but the digits must add up to a # divisible by “9”
o Anything ending in a “0” is also divisible by “10”
Objective 2: Find the prime factorization of a given number
•To find the prime factorization of a number , use a factor
tree
o Draw two branches below the number
o Place two factors that multiply to equal the given number at the end of the
two branches
o Repeat steps 1 and 2 for every composite factor
o Place all the prime factors together in a multiplication sentence
•Examples:

Objective 3: Find all possible factors of a given number
•This is called factoring which is simply a list of all of the possible factors of a given number
•Examples:
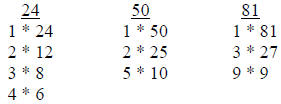
Objective 4: Find the greatest common factor of a give set of
numbers by listing
•To find the greatest common factor by listing
o List all the possible factors for each given number
o Search the lists for the greatest factor common to all lists
• Find the G. C. F. of: 24 and 60
Objective 5: Find the greatest common factor of a give set of numbers using prime factorization
•To find the greatest common factor of a given set of
numbers
o Write the prime factorizations of each number in exponential form
o Create a factorization for the G.C.F. that contains only those prime
factors common to all the factorizations
o Multiply
• Find the G. C. F. of: 24 and 60
Objective 6: Find the greatest common factor of a set of monomial
• Find the prime factorization of each monomial
• Treat the variables like prime number
• Find the G. C. F. of: 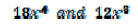
| Prev | Next |