Synthetic Division
Polynomial long division is a tedious process which can be
shortened considerably in
the special case when the divisor is a linear factor . By the factor theorem, if
we divide a
polynomial p (x) by the linear polynomial x − c, then p(c) is the remainder and
p(c) = 0 if
and only if (x − c) is a factor of p (x).
This observation suggest that in order to factor a polynomial p(x) of large
degree it
suffices to look for numbers c such that p(c) = 0. This is equivalent to long
division by
(x−c), which can be extremely drawn out . The method of synthetic division
accomplishes
division by a linear factor quickly and is done as follows:
Example Divide 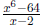
Begin as with polynomial long division but write only the coefficients of
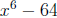 making
making
sure to list all of them.
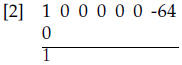
Carry the coefficient of the leading term as shown and
then multiply by c = 2, add to
the next column and repeat. Thus

The numbers below the line are the coefficients of a
polynomial of one degree lower , i.e.
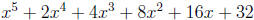 and the last number is the remainder.
Therefore,
and the last number is the remainder.
Therefore,
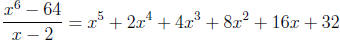
Observe that finding roots of any polynomial p(x) is now
reduced to finding a number
c (that would play the role of 2 above) such that the remainder of the synthetic
division ,
namely p(c), is zero .
Example Factor and find all roots of
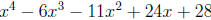
We begin with small test values c . Test first 1,−1, 2,−2, . . .. We have p(1) =
36, but
p(−1) = 0 and
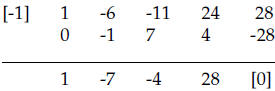
in other words we have performed the division
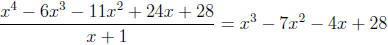
Repeating this process again with the newly obtained
polynomial we see that −2 works
and hence
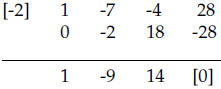
in other words we have performed the division
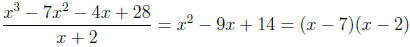
Therefore,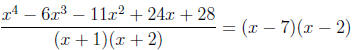
and 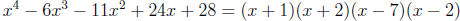
and the roots are {−2,−1, 2, 7}.
| Prev | Next |