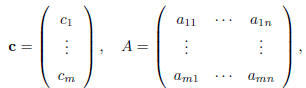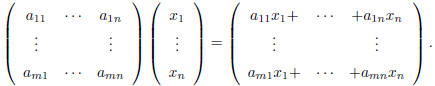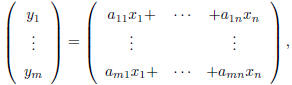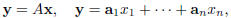System of Linear Equations
Slide 1
Definition 1 Fix a set of numbers
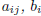 , where i = 1, ...,m and , where i = 1, ...,m andj = 1,... , n. A system of m linear equations in n variables 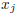 , is , isgiven by
Consistent: It has solutions (one or infinitely
many). |
Slide 2
| Solutions to a system of linear equations can be
obtained by: • Substitution. (Convenient for small systems.) • Elementary Row Operations . (Convenient for large systems.) It is not needed to write down the variable 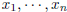 while whileperforming the EROs. Only the coefficients of the system , and the right hand side is needed. This is the reason to introduce the matrix notation. |
Slide 3
Matrix Notation
|
||||
Slide 4
| Elementary Row Operations (EROs) • Add to one row a multiple of the other . • Interchange two rows . • Multiply a row by a nonzero constant. EROs do not change the solutions of a linear system of equations. EROs are performed until the matrix is in echelon form. Echelon form: Solutions of the linear system can be easily read out. |
Slide 5
| Definition 2 The diagonal elements of a
matrix
are given by
|
Slide 6
| Echelon Forms • Echelon form: Upper triangular. (Every element below the diagonal is zero .) • Reduced Echelon Form: A matrix in echelon form such that the first nonzero element in every row satisfies both, - it is equal to 1, - it is the only nonzero element in that column. |
Slide 7
| Existence and uniqueness • A system of linear equations is inconsistent if and only if the echelon form of the augmented matrix has a row of the form 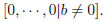 • A consistent system of linear equations contains either, - a unique solution, that is, no free variables, - or infinitely many solutions, that is, at least one free variable. |
Slide 8
| Vectors in IRn • Definition, Operations, Components. • Linear combinations. • Span. |
Slide 9
| Definition, Operations, Components Definition 3 A vector in IRn, n≥1, is an oriented segment. Operations: • Addition, Difference: Parallelogram law . • Multiplication by a number : Stretching, compressing. In components:
|
Slide 10
| Some properties of the addition and
multiplication by a scalar: u + v = v + u, u + (v + w) = (u + v) + w, a(u + v) = au + av, (a + b)u = au + bu. |
Slide 11
| Definition 4 A vector w ∈ IRn is a linear
combination of p≥ 1 vectors 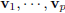 in IRn if there exist p numbers in IRn if there exist p numbers
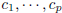 such suchthat 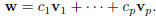 A system of linear equations can be written as a vector equation:
|
Slide 12
| Span Definition 5 Given p vectors 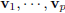 in IRn, denote by in IRn, denote bySpan 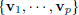 the set of all linear
combinations of the set of all linear
combinations of 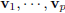 . .Note: • Span 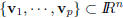 , ,• If w ∈ Span 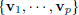 , then there exist
numbers , then there exist
numbers 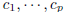 such that 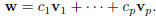 |
Slide 13
| Matrices as linear functions Definition 6 A linear function y : IRn →IRm is a function y(x) of the form
where
and |
Slide 14
| Introducing the vector c ∈ IRm, and the m n
matrix A as follows,
then, the linear function y(x) can be written as, |
Slide 15
| The product Ax is defined as follows:
Exercise: Show that this product satisfies the
following properties: |
Slide 16
| Summary A system of linear equations
can be expressed as a linear function, or as a
linear combination of |
Slide 17
Theorem 1 Fix and m n matrix
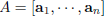 , and
a vector , and
a vectorb ∈ IRm. Then, b ∈ Span 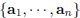
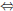 there exist there exist
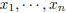 , such that , such that 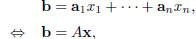  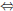 the echelon form of [A
l b] the echelon form of [A
l b] has NO row of the form has NO row of the form [0 ...0 l b ≠ 0]. [0 ...0 l b ≠ 0]. |
| Prev | Next |
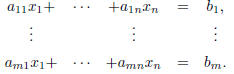
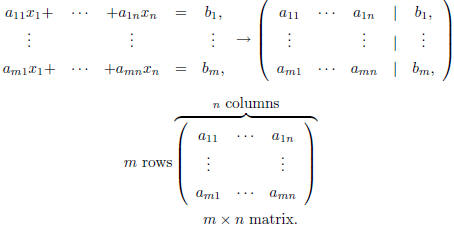
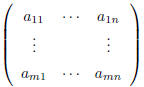
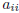 ,
for i from 1 to the minimum of m and n.
,
for i from 1 to the minimum of m and n.
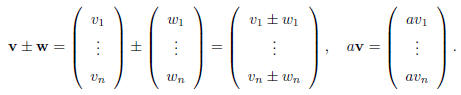
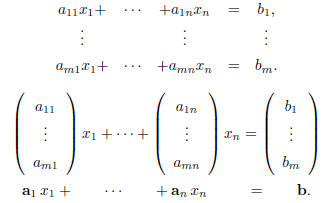
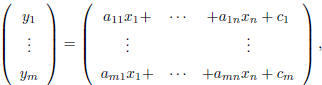
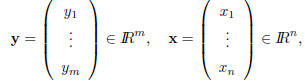
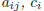 are constants, with i = 1, ,m, and j
= 1, n.
are constants, with i = 1, ,m, and j
= 1, n.