More Efficient Topological Sort
Abstract. Topological sort of an acyclic graph has
many applications such as job scheduling and network
analysis. Due to its importance, it has been tackledon many models. Dekel et al.
[3], proposedan
algorithm for solving the problem in O(log2N) time on the hypercube or
shuffle-exchange networks
with O(N3) processors. Chaudhuri [2], gave an O(logN) algorithm using
O(N3)
processors on a CRCW
PRAM model. On the LARPBS ( Linear Arrays with a Reconfigurable Pipelined Bus
System) model,
Li et al. [5] showed that the problem for a weighted directed graph with N
vertices can be solved
in O(logN) time by using N3 processors. In this paper, a more efficient
topological sort algorithm is
proposed on the same LARPBS model. We show that the problem can be solved in
O(logN) time by
using N3/ logN processors. We show that the algorithm has better time
and processor complexities than
the best algorithm on the hypercube, and has the same time complexity but better
processor complexity
than the best algorithm on the CRCW PRAM model.
Keywords: analysis of algorithms, graph problem, massive parallelism, optical bus, time complexity
1. Introduction
Many applications can be represented as an acyclic graph.
The topological sort of
an acyclic graph is to find a linear ordering for the vertices of the graph, such
that
if <i j> is an edge of the graph, then i appears before j in the ordering [4].
If
the graph is not acyclic then no linear ordering is possible. A topological sort
of a
directed graph can be viewed as an ordering of its vertices along a horizontal
line, so
that all directed edges go from left to right. Topological sort has many
applications
in various job scheduling, network analysis, and other areas [1, 4].
The topological sort problem has been tackled on many
models. For example,
Dekel et al. proposed an algorithm for solving the problem in O(log2N) time on
the
hypercube or shuffle-exchange networks with O(N3) processors [3]. Chaudhuri also
gave an O(logN) algorithm using O(N3) processors on a CRCW PRAM model [2].
In this paper, we study the problem on a new computational model called Linear
Array with a Reconfigurable Pipelined Bus System (LARPBS) [10], which will be
briefly discussed below. Since an LARPBS can simulate a primitive operation on
a hypercube with the same number of processors in O(1) time, the algorithm on
the hypercube reported in [3] can be implemented on an LARPBS with the same
time and process or complexities. The question is: can we do a better job through
direct implementation on the LARPBS model? Recently, an algorithm using optical
buses was proposed in [7]. The topological sort algorithm is based on the matrix
of
all-pairs shortest paths. The problem with this method , is that the time
complexity
of the algorithm is related to the magnitude of weights associated with a graph.
For weights of unbounded magnitude, the time complexities with the algorithms
are normally larger. Li et al. [7] showed that the problem for a weighted directed
graph with N vertices can be solved in O(logN) time by using N3 processors, if
the weights are of bounded magnitude and precision. For weights of unbounded
magnitude and precision, the problem can be solved in O(logN) time by using
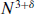 (where is any small positive constant) processors; in O( logN log logN)
(where is any small positive constant) processors; in O( logN log logN)
time by using N3/ log logN processors; or in O(logN) time with high probability
by using N3 processors. In this paper, we implement a topological sort algorithm
on the LARPBS based on the approach for computing the transitive closure of a
graph. Because transitive closure of a graph is calculatedbasedon boolean
values,
more efficient algorithms can be achieved compared with calculations based on
integer values. Our algorithm solves the same problem in O(logN) time by using
only N3/ logN processors, and is better than the one in [7] on the same model.
Our result also shows, that not only better time bounds are obtained, but also
fewer processors are used for the same problem on the LARPBS model, than the
algorithm on the hypercube model described in [3]. Our algorithm has the same
time bound, but uses fewer processors than the algorithm on the CRCW PRAM
model [2].
It should be noted that Ma et al. [8], claimed that the
topological sort problem
can be solved in O(1) time based on the transitive closure algorithm on a 2D
reconfigurable mesh with N3 processors described in [15]. However, their
transitive
closure algorithm works only for undirected graphs, and topological sort requires
a
solution for directed graphs. Hence, there is a flaw in the algorithm described
in
[8]. Since the transitive closure problem on undirected graphs is much easier
than
directed graphs, it is not clear whether the topological sort problem can be
solved
in O(1) time on a 2D reconfigurable mesh. For 1D arrays, such as the LARPBS
model, the problem seems to be more difficult to solve, since we cannot embed a
graph into the architectures for a fast solution.
2. Reconfigurable pipelined optical buses
Recent advances in optical technologies have made optical
interconnection networks
feasible. A pipelined optical bus system uses optical waveguides instead of
electrical signals to transfer messages among electronic processors. In addition
to
the high propagation speed of light, there are two important properties of
optical
pulse transmission on an optical bus, namely, unidirectional propagation and
predictable propagation delay. These advantages of using
waveguides enable synchronized
concurrent
accesses of an optical bus in a pipelined fashion [9].
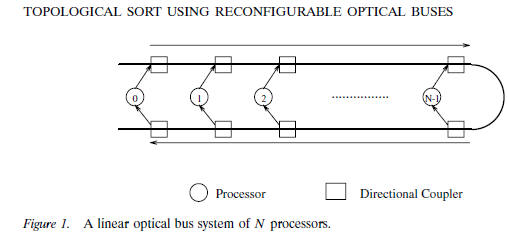
Figure 1 shows a linear array in which electronic
processors are connected with
an optical bus. Each processor is connected to the bus with two directional
couplers,
one for transmitting on the upper segment, and the other for receiving from
the lower segment of the bus [9–11]. The optical bus contains three identical
waveguides,
one for carrying messages (the message waveguides), and the other two for
carrying address information (the reference waveguide and the select waveguide).
For
the purpose of simplicity, the message waveguide, which resembles the reference
waveguide, has been omitted. As shown in Figure 1, only the reference waveguide
and the the select waveguide are displayed there. Messages are organized as
fixed length
message frames. Note that optical signals propagate unidirectionally from left
to right on the upper segment, and from right to left on the lower segment. This
bus system is also referred to as the folded-bus connection in [10].
The three waveguides are used for addressing and simple
computations , such as
binary value summation [10]. It has been shown that such pipelinedoptical bus
systems can support a massive volume of communications simultaneously, andare
particularly appropriate for applications that involve intensive regular or
irregular
communication andd ata movement operations, such as permutation, one-to-one
communication, broadcasting, multicasting, multiple multicasting, extraction,
and
compression [6, 10]. It has been shown that by using the coincident pulse
addressing
technique, all these primitive operations take O(1) bus cycles, where the bus
cycle
length is the end-to-end message transmission time over a bus [6, 10].
Remark To avoid controversy, let us emphasize that
in this paper, by “O(f(p))
time” we mean O(f(p)) bus cycles for communication plus O(f(p)) time for local
computation.) This assumption has been used by many other authors in the
literature
[6, 9, 11–14] for different models with optical buses.
In addition to supporting fast communications, an optical
bus itself can be used
as a computing device for global aggregation. It was proven in [6, 10], that by
using
N processors, the summation of N integers or reals with bounded magnitude and
precision, the prefix sums of N binary values, the logical-or and logical-and of
N
Boolean values can be calculated in constant number of bus cycles.
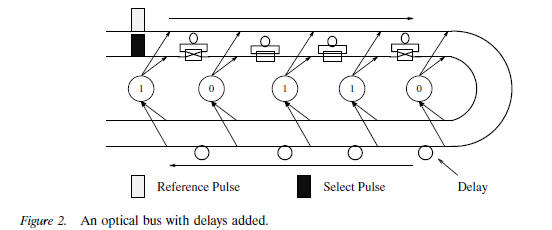
An LARPBS consists of N processors
 connected by a
pipelined
connected by a
pipelined
optical bus. In the LARPBS, we insert an optical switch on each section of the
transmitting
bus and receiving bus. Thus, each processor has 6 more local switches, three
on its three receiving segments, and three on its three transmitting segments,
besides
its switch for conditional delay. The switches on the receiving and transmitting
segments
between processors i and i + 1 are called RSR(i) and RST(i), respectively,
and are local to processor i as shown in Figure 2. Here, RSR(i) 0 ≤ i < N are
2 × 1 optical switches, and RST(i) 0 ≤ i < N are 1 × 2 optical switches. In the
following
discussion, these switches, will be called reconfigurable switches, due to their
function. When all switches are set to straight, the bus system operates as a
regular
pipelined bus system. When RSR(i) and RST(i) are set to cross, the whole bus system
is split into two separate systems, one consisting of processors 0,1,...., and i
and the other consisting of i +1, i +2, ... , N −1. Thus, in general an LARPBS can
also be partitioned into k ≥ 2 independent subarrays LARPBS1, LARPBS2,
... ,
LARPBSk, such that LARPBSj contains processors
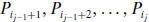 , where
, where
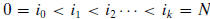 . The subarrays can operate as regular linear arrays
. The subarrays can operate as regular linear arrays
with pipelined optical bus systems, and all subarrays can be used independently
for
different computations without interference (see [10] for an elaborated
exposition).
Figure 3 shows the LARPBS model with 6 processors. The array is split into two
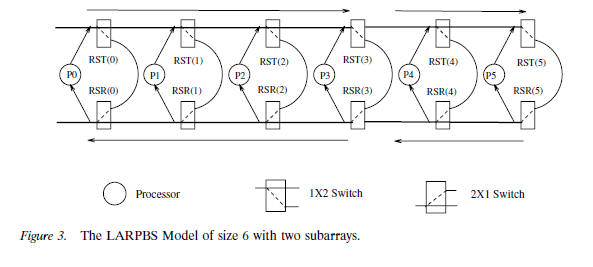
subarrays, with the first one having four processors,
and the second one having two
processors.
As pointed out in [10], many intensive regular or irregular
communication
and data movement operations, such as permutation, one-to-one communication,
broadcasting, multicasting, multiple multicasting, extraction, and compression
can
be carried out in O(1) bus cycles on an LARPBS. The above primitive communication,
data movement, and aggregation operations provide an algorithmic view
on parallel computing using optical buses, and also allow us to develop, specify,
and analyze parallel algorithms by ignoring optical and engineering details. These
powerful primitives that support massive parallel communications, plus the
recon-figurability
of optical buses make the LARPBS computing model very attractive in
solving problems that are both computation and communication intensive. See [6,
9,
11–14] for more algorithms on the LARPBS model and some related models using
optical buses.
3. Topological sort on the LARPBS model
In this section, a new topological sort algorithm is
described on the LARPBS model.
The previous primitive operations are used as building blocks in our
implementation.
Before we describe the algorithm, we need to present some
terms and notation .
The connectivity matrix of a graph G with N vertices is an N × N matrix C, whose
elements are defined as follows: cjk
= 1 if there is path from vertex j to k (j ≠ k), or
vertex j is the same as vertex k (i.e., j = k). Otherwise, cjk=0 for 0 ≤ j k ≤ N
− 1.
The matrix C is also known as the transitive closure of the graph G. Li [5], has
shown
that the product of two N × N boolean matrices can be calculated in constant time
on an LARPBS with O(N3)/ logN processors. The algorithm is a parallelization of
the Four Russians’ algorithm. Further, the time complexity of the algorithm is
measured by
bit level operations. By using the boolean matrix multiplication algorithm
O(logN) times, Li has also established the following result [5]:
Lemma 1 [5] The transitive closure of a graph with N
vertices can be computed in
O(logN) bus cycles on an LARPBS with N3/ logN processors.
Let G = (V,E) be a connected directed graph with N vertices.
For any two
vertices j and i, we say that i is j-reachable, and i is a predecessor of j if
there
is a path from i to j in G. G = (V,E) is called a dense graph if E = O(N2
). For
vertix i, define two sets
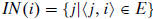 ,
and
,
and
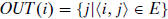 . Then,
. Then,
In-degree(i) =|IN(i)| andOut-degree(i)= |OUT(i)| .
Let AC(v) = {x |x is v—reachable in G and Num(v)= |AC(v)| , the
following
lemma is due to [8]:
Lemma 2 Assume that G is a directed acyclic graph,
and v, and w are two vertices
of the graph. If v is a predecessor of w, then Num(v) > Num (w).
The correctness of this lemma can be explained intuitively.
Because v is a predecessor
of w, there is a directed path of length at least one from v to w . Clearly, for
any vertex u, if u is w-reachable, u is also v-reachable. Hence, we have Num(v) >
Num (w) .
In [10], a quicksort algorithm using an average of O(logN)
bus cycles on an
LARPBS with N processors is described. The quicksort algorithm is suitable for
general keys. If we restrict the values to integers, a radix sorting algorithm
can be
used. We show here that an LARPBS with N processors can sort N integers with
k bits in O k steps. The basic idea is to repeat the split operation (a
generalized
compression operation) k times , and each time uses the l-th bit as the mark for
the active set, where 0 ≤ l < k [10]. After k iterations, all N integers are in
sorted
order. Since vertices in a graph use integer representation, radix sort is
suitable for
most graph problems as shown below. We repeat the lemma here.
Lemma 3 A radixsort of N integers with logN bits
can be performed in O(logN)
bus cycles.
Assume that a matrix is stored in a row-major fashion in an
LARPBS. That is,
element i j is stored in processor k, where k = N * i + j. The transpose of a
matrix involves storing the matrix in column-major fashion. This can be easily
done
through exchanging the two indices and calculate the new location for an
element.
Then, each processor just sends the element to the destination processor. This
can
be performed in O(1) bus cycles.
Lemma 4 A transposition of a matrix can be carried
out in O(1) bus cycles assuming
that each processor stores one element of the matrix.
Our algorithm is based on the above results. The input of
our algorithm is the
adjacency matrix A of a directed graph G = (V,E) , where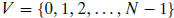 .
.
The output of our algorithm has two possibilities. If there is a directed cycle
in G,
the algorithm indicates a failure and exits immediately. Otherwise, the result
for
topological sort is stored in the array 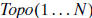 such that if v is a predecessor
such that if v is a predecessor
of w and Topo(i) = v and Topo (j) = w, then i < j. That is, Topo(i) points to node
v which has a rank i in the topological order.
Our algorithm uses an LARPBS with N3/ logN processors.
Assume that the
adjacency matrix A is stored in the first N2 processors in row-major order. The
algorithm consists of the following 7 steps:
Proposed Algorithm
• Step 1: A = A + I, where I is the N × N unit Boolean
matrix. This can be
done in O(1) time, since each processor holding a diagonal element sets its local
element in A to one.
• Step 2: Calculate the transitive closure A* of A via logN time Boolean matrix
multiplication. This step can be carried out in O(logN) bus cycles on an LARPBS
with N3/ logN processors.
• Step 3: If there exist a pair of vertices such that A* (i,j) ∧ A*
(j,i) = 1, then
output “None” and exit; otherwise, continue to next step. This step can be
carried
out easily by a matrix transposition operation and can be done in O(1) bus cycles
based on lemma 4.
• Step 4: Calculate the vector

Basically, Num(v) contains the row sum of A*. We can
reconfigure the subarray
with the first N2 processors into N subsystems, where each subsystem contains
an LARPBS with N processors.
Then perform a summation in each subsystem in parallel
using the bus split
method, and store the sum in the first processor of each subsystem. Move the N
sums to the first N processors in the LARPBS. Hence, this step requires at most,
logN bus cycles.font>
• Step 5: Construct a 2-dimensional array B (0...N −1,1...2)
such that B(v,1) =
Num(v) , and B(v,2) = v for 0 ≤ v ≤ N − 1. The array B is stored in the first N
processors of the LARPBS. This step takes a constant time.
• Step 6: Sort the array B, based on the following rule : for any i j, 0 ≤ i j ≤ N
−1,
 . We can use the
. We can use the
radix sorting algorithm on the LARPBS model [10], to sort the array B. Since the
value of the array B elements has at most O(logN) bits, this step can be done
in O(logN) bus cycles.
• Step 7: Copy the results into array Topo; i.e; Topo(t) = B (t,2). Here, only
local
operations are involved. This is done in parallel and hence takes O(1) time.
The final results are in the Topo variables of the first N
processors of the
LARPBS. The correctness of this algorithm can be intuitively explained as
follows.
First, if there is a directed cycle via vertices i and j, by the definition of
A*, it
must be true that A*(i,j) = 1 and A*(j,i) = 1. Hence, the algorithm should exit in
Step 3. Otherwise, the vertices of G are arranged in array
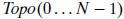 according
according
to the decreasing order of Num(v) . In other words, for any two vertices i and
j, assume Topo(i) = v and Topo(j) = w, if Num(v) ≥ Num (w) , then i < j. Based
on Lemma 2, the vertices of G are listed in topological order.
According to the above analysis, the total time used in
the algorithm is O(logN)
bus cycles. Hence, we have the following theorem:
Theorem 1 The topological sort problem can be
solved in O(logN) bus cycles on an
LARPBS with N3/ logN processors.
4. Conclusions
In this paper, a new and improved topological sort algorithm
has been presented
on the LARPBS model. The algorithm has better performance compared with their
counterparts on the hypercube [1], and on the theoretical CRCW PRAM model [2].
It also improves an algorithm on the same model reported in [7]. The standard
sequential topological sort algorithm has a time complexity of O N + E in a
directed graph G N E [2]. In the worst case, it is O N2 time. Hence, our
algorithm
is still not optimal in terms of time-processor product. Further reduction in
processor complexity in the algorithm would be an interesting research topic.
Acknowledgments
Research was supported in part by the Ministry of
Education, Science, Sports and
Culture of Japan under Grant-in-Aid for Scientific Research (C), No.1168041, and
by the Japan Society for Promotion of Science in the form of a fellowship, the
National Science Foundation (NSF) under Grant CCR-9503882.
| Prev | Next |