Final Exam
1. ( Change of coordinates ) Suppose x=au+bv+cw, with
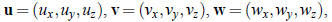
and x = (x, y, z) in some coordinate system .
(a) Write the coordinates of x = (x, y, z) in terms of the coordinates of u, v, and w.
(b) Write the coordinates from part (a) in the form
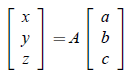
where A is a 3*3 matrix
(c) Now suppose the coordinates of x = (x, y, z) are known, and given the
coordinates of some u, v,
and w, we wish to find a, b, and c such that x = au+bv+cw. How can they be
computed?
2. (Orthogonal change of coordinates) Continuing the previous problem ,
suppose u, v, and w are perpendicular
(orthogonal), i.e., u*v = 0, u*w = 0, and v*w = 0.
(a) compute ATA.
(b) If, in addition to being orthogonal, u, v and w are unit vectors, what is ATA?
(c) Use the result from part (b) to solve the equation
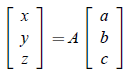
for a, b, and c.
(d) Use the result from part (a) to solve the equation if u , v, and w are
orthogonal but not not necessarily
unit vectors.
3. (3*3 matrix inversion)
The previous exercises show how to compute the inverse of a matrix with
orthogonal columns: the
key property is that A TA is a diagonal matrix, and hence is a small step from
the identity matrix. This
is a special property of orthogonal matrices, for general matrices, it does not
hold. However, if we
can construct a matrix B such that BTA is a diagonal matrix, the inverse of A is
not far off.
Let
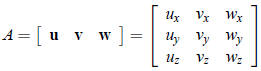
(a) Suppose B is some 3*3 matrix
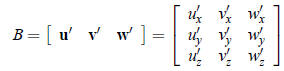
Show that
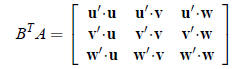
(b) The matrix BTA is a diagonal matrix if u' is perpendicular to v and w,
v'
is perpendicular to u
and w, and w' is perpendicular to u and v. In this case, the vectors u', v', and
w' are said to be dual to
u, v, and w.
Explain why the vectors
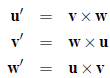
are dual to u, v, and w. (You may refer to a problem on the previous homework assignment.)
(c) With u', v', and w' as computed from u, v, and w as above, the product
matrix BTA is a diagonal
matrix, but not the identity matrix. For what scalars a, b, and c does the
matrix C having columns au',
bv' , and cw' produce CTA = I? (Hint: look at the code for matrix3d::inverse()
if you get stuck.)
(d) Express the scalars a, b, and c directly in terms of the coordinates of
u, v, and w, and show that
they all have the same value. Show that this common value is the determinant of
A. (You may want
to refer to the scalar triple product problem from the previous homework.)
(e) It follows from the previous part that
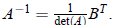Write out BT in terms of the entries of A,
thereby providing a direct formula for the inverse of A.
4. The cosine of the angle between two vectors u and v is defined as
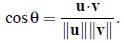
The C++ acos function can be used to compute q from this expression. One
might try the following
C++ code for this:
float theta = acos(u.dot(v)/(u.length()*v.length())),
Is this guaranteed to work? Why or why not?
5. Although it is common to use the term “line” in graphics for the output of
Bresenham’s midpoint
line-drawing algorithm, it has its shortcomings as a representation of a
mathematical line , or even a
“line” drawn with pen on paper. Describe at least two such shortcomings.
6. Bresenham’s midpoint line-drawing algorithm, as given in class, uses only
integer arithmetic to draw a
line between two points having integer coordinates. Explain how the algorithm
could be modified for
points having general floating-point coordinates. Is it possible to do so using
only integer arithmetic?
7. The function for the midpoint circle algorithm you implemented in the
second lab assignment expected
three (integer) arguments: x0, y0 for the coordinates of the center of the
circle, and r for the
radius. The draw crude circle function, however, used the (integer) coordinates
x1, y1 of a point
on the circle instead of the explicit radius.
(a) Write a C++ expression for the radius of a circle centered at x0, y0,
through the point x1, y1,
appropriate for your Bresenham circle function. (Remember that the radius has to
be an integer).
(b) If your Bresenham circle algorithm had to call the draw crude circle
function (perhaps to
compare the result with the midpoint algorithm) what parameters would you pass
to draw crude circle,
to guarantee the same radius?
(c) Find an example of two points (x0, y0) and (x1, y1) for which the circle
centered at (x0, y0) through
(x1, y1) has a non-integer radius. Is there an example for which the square of
the radius is not an
integer?
(d) Could the Bresenham circle algorithm be modified to use a point on the
circle, given by integer
values x1 and y1, instead of the (integer) radius and still use only integer
arithmetic? Explain. (Remember
that there are essentially two parts: what pixel to start with and whether to
proceed “East” or
“Southeast” at each iteration of the loop.)
8. One possible alternative to the even-odd rule for filling general polygons
would be to fill all the
pixels between the outermost active edges at each scanline. Would this provide a
satisfactory filling
algorithm in general? How would it perform on convex polygons?
9. While filling a general polygon by triangles is possible, it involves
significant extra computation. On
the other hand, the general scanline polygon fill algorithm works as it stands
for filling triangles. What
advantages are there to using the barycentric triangle algorithm over the
general polygon algorithm for
filling triangles? Are there any drawbacks to using the barycentric version?
Does it make a difference
if the triangle contains only a few pixels, or if it contains a large number of
pixels ?
You need not go through a detailed algorithm analysis, a qualitative
comparison is fine. (Actually, it is
not fair to compare the two algorithms directly, as the general polygon
algorithm can be made much
more efficient than was presented in class).
| Prev | Next |