Inverse Functions
Defining Inverse Functions
In our final lecture of the term , we discuss the concept of the inverse of a
function. Let f(x) be a real-valued
function. We say that g(x) is the inverse of f(x) if for all values of x in the
domain of f(x), we have that
g(f(x)) = x,
and for all values of x in the domain of g(x), we have that
f(g(x)) = x.
So composing g after f cancels out the action of f, and composing f after g
cancels out the action of g. We
usually denote the inverse of f(x), if it exists, by f-1(x). If f(x) is the
inverse of g(x), then g(x) is also the
inverse of f(x).
We already have an important example of inverse functions. the inverse of the
exponential function ex is
the natural logarithmic function ln x, since for all real numbers x, we have
that
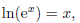
and for all values of x in the domain of ln x (what is this domain?) we get that
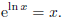
Likewise, the functions ax and logax are inverses to each other, because we
defined logax specifically to
have this property .
Another example of inverse functions are xn when n is a odd natural number and
the nth root function
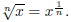Both of these functions are defined everywhere, and we have that
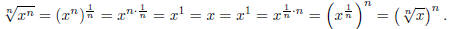
This concept of inverse function gets a little more tricky
when we consider the function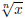 
when n is an
even natural number ( like the usual square root function). The function
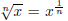is always non-negative
(that is, positive or 0). This restriction makes an impact on the domain of the
inverse function. we would
guess that xn would be the inverse to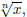 
and
this is true, but xn is defined for all real numbers. If x is a
negative number, then
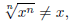
because x is negative, but the nth root of any number is
non -negative when n is an even number. Thus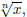
does not cancel out the action of xn when x is a negative number. The solution
is to restrict the domain
of xn to non-negative numbers, and, indeed, xn on the domain x ≥ 0 is the
inverse function of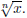 
The
lesson here is that we always need to be conscious of the domain of a function
as well as its formula, because
studying the formula alone can give us the wrong answer.
Some functions do not have inverse functions. for these
functions, there is no way to cancel out their
action on x, to put the machine into reverse, once that action is done. Chief
among these functions are the
constant functions f(x) = c. A constant function sends every number x to some
constant c. If g(x) were the
inverse to f(x) = c, then for every value of x we would have that
x = g(f(x)) = g(c).
So g(c) would have to have every real number as a value,
which is impossible, because as a function, g(c) can
take exactly one value and one value only. So constant functions cannot have
inverse functions. Likewise,
consider the function f(x) = x2 defined everywhere. If g(x) is the inverse of
f(x) = x2, then, specifically,
for x = 1 and x = -1 we would have
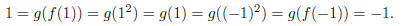
Thus if g(x) is the inverse function of f(x) = x2 (defined
everywhere), then both g(1) = 1 and g(1) = -1,
which is impossible if g(x) is indeed a function. So f(x) = x2 defined
everywhere does not have an inverse.
We can restrict its domain, however, as we saw in the previous paragraph , and
get a function which does
have an inverse. Why does f(x) = x2 defined everywhere not have an inverse,
while f(x) = x2 defined on
the non-negative numbers does? We examine their graphs to find out .
Graphs of Inverse Functions and the Horizontal Line Test
The graph of a function and the graph of its inverse are
related. To see this relationship, plot the graph of
ex and the graph of ln x on the same set of axes. Now plot the line y = x. What
you should see is that
the graph of ex and the graph of ln x are exact reflections of each other in the
line y = x. This is true not
just for ex and ln x, but for the graphs of f(x) and f-1(x) as well. the graph
of f-1(x), when this function
exists, is the reflection of the graph of f(x) in the line y = x.
Why is this the case? When we reflect the point (x, y) in
the line y = x, we get the point (y, x) (test this
on a few points to convince yourself of this). Every point on the graph of f(x)
is of the form (x, f(x)), so
every point in the reflection of the graph of f(x) in the line y = x is of the
form (f(x), x). If the reflection
is the graph of a function, then this function takes f(x) and sends it to x for
every x in the domain of f,
which is precisely what the inverse function is supposed to do.
Thus, knowing what the graph of x3 looks like, you should
be able to draw the graph of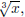 
, and knowing
how to draw the graph of x2 for x ≥ 0, you should be able to sketch the graph of
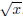
What about the constant function f(x) = c? The graph of
this function is a horizontal line. Therefore,
if we reflect the graph of f(x) = c in the line y = x, we get the vertical line
x = c. This vertical line cannot
be the graph of a function, since it obviously does not pass the vertical line
test. So this graphically justifies
why we say that constant functions do not have inverses.
What about the function f(x) = x2 defined everywhere? When
we reflect it in the line y = x, the result
is the solution curve of the relation x = y2, which is a parabola on its side.
If you sketch this solution
curve, you see that it does not pass the vertical line test either, particularly
at x = 1, as we showed before
algebraically . So f(x) = x2 defined everywhere does not have an inverse either.
These two examples give us a clue as to a test we can use
to see it a function does not have an inverse.
In both of these cases, the reflection of the graph of the function failed the
vertical line test. some vertical
line x = a passed through the reflection at two points or more. What does this
tell us about the graph
of the original function? Try reflecting back the vertical line x = a. you get
the horizontal line y = a.
Superimpose this horizontal line onto the graph of the original function. You
should see that it crosses the
graph of the original function at two or more points. So, if the reflection of
the graph of a function fails
the vertical line test, then some horizontal line passes through the graph of
the function more than once,
and vice versa. This is the horizontal line test. if f(x) is some real-valued
function and there exist some
horizontal line y = a which passes through the graph of f(x) more than once (in
other words, f(x) = a for
more than one value of x), then f(x) does not have an inverse. Thus f(x) = x2
defined everywhere does not
have an inverse because its graph, a parabola open upward, certainly does not
pass the horizontal line test.
The graph of the absolute value function does not pass the horizontal line test,
and neither does any of the
trigonometric functions , so none of these functions have inverses. If we
restrict these functions to smaller
domains, however, as we did by restricting f(x) = x2 to the non-negative
numbers, then these function may
have inverses on these smaller domains. This is, for example, how we define the
inverses of the trigonometric
functions, which you will study in detail next term.
| Prev | Next |