MATHEMATICS COMMON ASSESSMENT REVIEW
Identify the letter of the choice that best completes the statement or answers the question.
1. Evaluate g (n – 9)
if 
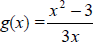
2. Find all real zeros
of the function y = -7x + 4.
3. Find an equation in
slope -intercept form of the line that has slope 2 and passes
through point A(-8, 7).
4. Determine the
standard form of the equation of the line that passes through (-4, 7)
and (8, 0).
5. Which statement best describes a method that can be used to sketch the graph?
y = |x + 1|
a. Translate the graph of y = |x| one unit right.
b. Translate the graph of y = |x| one unit down.
c. Translate the graph of y = |x| one unit up.
d. Translate the graph of y = |x| one unit left.
6. Without graphing, describe the end behavior of the graph of the function.
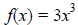
7. Use the remainder theorem to find which of the following is not a factor of
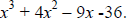
8. Solve.
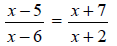
9. Solve.
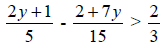
10. Determine the equation whose roots are 2, 4, and -5.
11. Solve x 3 + 3x2 + x – 5 = 0.
12. Find the number of possible negative real zeros of f(x) = 2x4 + 14x3 – 35x2.
a. three
b. two
c. one
d. none
Short Answer
13. State the domain and range of {(7, -6), (-1, 6), (-1, 0)}, and determine
whether the relation is
a function.
14. Determine the domain of the function. Make a number line, and answer in
interval notation.
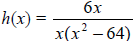
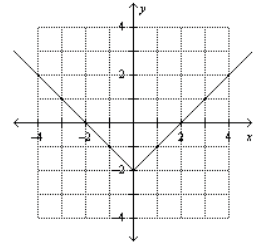
15. Use the graph to determine the domain and range of the
relation in interval notation, and state
whether the relation is a function.
16. Find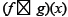 
if f(x) = x2 + 4 and g(x) = 3x – 2.
17. Determine whether the graphs of y = -5x + 17 and
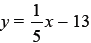are parallel, perpendicular,
coincident, or none of these.
18. Write an equation for a line in slope - intercept form that is parallel to the
graph of y = 5x + -2
and passes through the point at (-5, 3).
19. Write an equation for a line in slope-intercept form that is perpendicular
to the graph of
8x – 2y = 7 and passes through the point at (-8, 9).
20. Is the following function an even function, an odd
function, or neither?
y = -3x2 – 6x
21. The graph below is a portion of a complete graph. Sketch the complete graph
assuming it is
symmetric with respect to the y-axis.
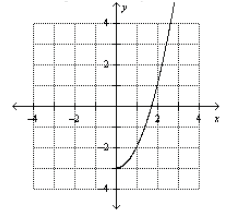
22. Find the inverse of: f(x) = (x -2)3.
23. Solve x2 – 2x = 35 by completing the square.
24. Find the discriminant and describe the nature of the roots of 4x2 + 2x + 6 =
0.
25. Solve 2x2 + 2x – 2 = 0 using the quadratic formula.
26. Find (x3 + 3x2 – 4x - 8) ÷ (x + 2) by using synthetic division.
27. List the possible rational roots of 2x3 + x2 – 13x + 6 = 0.
28. Find all the zeros of f (x) = 2x3 – 7x2 + x + 10.
Solve.
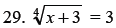
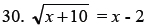
Identify the change in the parent function that will
produce the related function shown as a
dashed line.
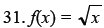
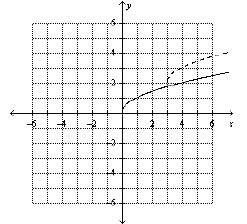
32. f(x) = |x|
33. Find the number of complex roots of x3 + x2 – 2x = 0.
Then find the roots and graph the
related function.
34. Locate the asymptotes, find the x and y intercepts,
and graph the rational function
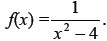
Graph.
35. y < |2x + 8|
Make a T-table.
36. f(x) = x4 – 4x2
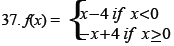
Use a graphing calculator to complete each of the
following.
38. Approximate to the nearest tenth the real zeros of f (x) = -5x3 + 9x2 + 12x
+ 2 .
39. Find the relative minimum and the relative maximum points to the nearest
tenth for the graph
of f (x) = -x3 + 3x2 + 9x - 9 .
40. Find the relative and absolute maxima and minima to the nearest tenth of
f (x) = 2x4 + x3 - 11x2 - 4x + 12 .
| Prev | Next |