PRACTICE PROBLEMS
Find the root if it is a real number.
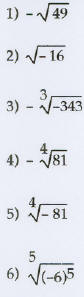

Simplify the expression involving rational exponents .
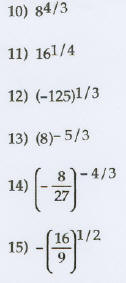
Write with radicals. Assume that all variables represent
positive real numbers.
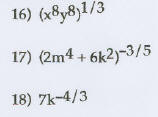
Simplify by first converting to rational exponents. Assume
all variables represent positive real numbers. Give the
answer in radical form.
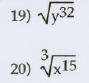
Use the rules of exponents to simplify the expression.
Write
the answer with positive exponents. Assume that all
variables represent positive real numbers.
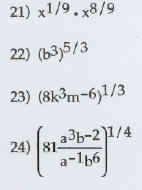
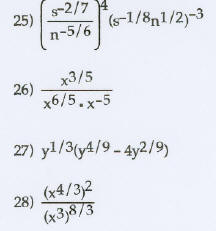
Write with rational exponents, and then apply the
properties
of exponents. Assume all radicands represent positive real
numbers. Give answer in exponential form .
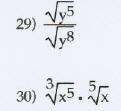
Simplify the radical. Assume that all variables represent
positive real numbers.
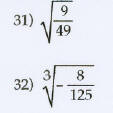
Express the radical in simplified form.
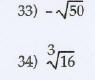
Express in simplified form. Assume that all variables
represent positive real numbers.
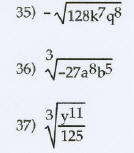
Simplify the radical. Assume that all variables represent
positive real numbers.
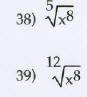
Perform the indicated operations and simplify . Assume that
all variables represent positive real numbers.
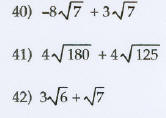
Simplify. Assume that all variables represent positive
real
numbers.
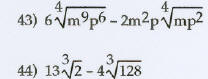
Multiply, then simplify the product. Assume that all
variables represent positive real numbers.

Rationalize the denominator. Assume that all variables
represent positive real numbers.
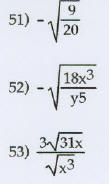
Simplify. Assume that all variables represent positive
real
numbers.
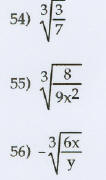
Rationalize the denominator. Assume that all variables
represent positive real numbers and that the denominator is
not zero.
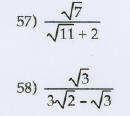
Write the expression in lowest terms . Assume that all
variables represent positive real numbers.
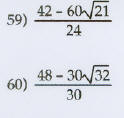
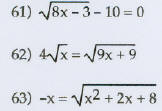
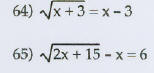
Solve this equation.
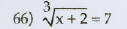
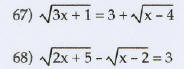
Write the number as a product of a real number and i.
Simplify the radical expression.
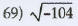
Multiply or divide as indicated .
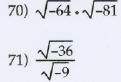
Add or subtract as indicated. Write your answers in
standard
form.
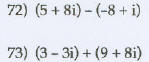
Multiply.

Use the square root property to solve the given equation.
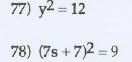
Use the quadratic formula to solve the given equation.
( Solutions are real numbers.)
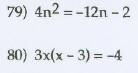
Use the quadratic formula to solve the given equation
Answer Key
Testname: 100PRACTICEPROBSTEST4 SPR06

| Prev | Next |