The Quadratic Formula
Intercepts
In Example 13, we used the quadratic formula to
find the solutions of x2 − 2x − 2 =
0. These solutions, and their approximations, are shown in equation (14).
It is
important to make the connection that the solutions in equation (14) are
the zeros
of the quadratic function g(x) = x2 −2x−2. The zeros also provide the
x-coordinates
of the x-intercepts of the graph of g (a parabola). To emphasize this point,
let’ s draw
the graph of the parabola having the equation g(x) = x2 − 2x − 2.
First, complete the square to place the quadratic function in vertex form. Take
half
the middle coefficient and square , as in [(1/2)(−2)]2 = 1; then add
and subtract this
term so the equation remains balanced.
g(x) = x2 − 2x − 2
g(x) = x2 − 2x + 1 − 1 − 2
Factor the perfect square trinomial , then combine the
constants at the end.
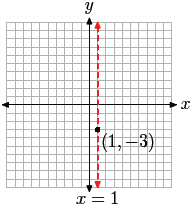
g(x) = (x − 1)2 − 3
This is a parabola that opens upward. It is shifted to the right 1 unit and down
3 units.
This makes it easy to identify the vertex and draw the axis of symmetry, as
shown in
Figure 1(a).
It will now be apparent why we used our calculator to approximate the solutions
in (14). These are the x-coordinates of the x-intercepts. One x-intercept
is located at
approximately (−0.73, 0), the other at approximately (2.73, 0). These
approximations
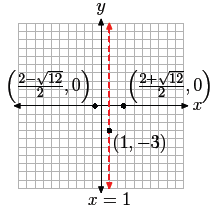
are used to plot the location of the intercepts as shown in Figure 1(b).
However, the
actual values of the intercepts are ((2−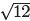 )/2,
0) and ((2+
)/2,
0) and ((2+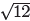 )/2, 0), and these exact
)/2, 0), and these exact
values should be used to annotate the intercepts, as shown in Figure 1(b).
Finally, to find the y-intercept, let x = 0 in g(x) = x2 − 2x − 2.
Thus, g(0) = −2
and the y-intercept is (0,−2). The y-intercept and its mirror image across the
axis of
symmetry are both plotted in Figure 1(c), where the final graph of the
parabola is
also shown.
 |
 |
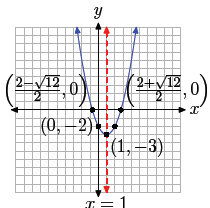 |
| (a) Plotting the vertex and axis of symmetry. |
(b) Adding the x-intercepts provides added accuracy. |
(c) Adding the y-intercept and its mirror image provides an excellent final graph. |
We’ve made an important point and we pause to provide emphasis.
Zeros and Intercepts. Whenever you use the quadratic formula to solve the
quadratic equation
ax2 + bx + c = 0,
the solutions
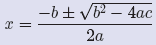
are the zeros of the quadratic function
f(x) = ax2 + bx + c.
The solutions also provide the x-coordinates of the x-intercepts of the graph of f.
We need to discuss one final concept.
The Discriminant
Consider again the quadratic equation ax2 + bx + c = 0 and the
solutions (zeros)
provided by the quadratic formula
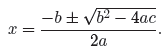
The expression under the radical , b2 −4ac, is called the discriminant,
which we denote
by the letter D. That is, the formula for the discriminant is given by
D = b2 − 4ac.
The discriminant is used to determine the nature and number of solutions to the
quadratic
equation ax2+bx+c = 0. This is done without actually calculating the
solutions.
Let’s look at three key examples.
 Example 15. Consider the quadratic equation
Example 15. Consider the quadratic equation
x2 − 4x − 4 = 0.
Calculate the discriminant and use it to determine the nature and number of the
solutions.
Compare x2 − 4x − 4 = 0 with ax2 + bx + c = 0 and note
that a = 1, b = −4, and
c = −4. The discriminant is given by the calculation
D = b2 − 4ac = (−4)2 − 4(1)(−4) = 32.
Note that the discriminant D is positive; i.e., D > 0.
Consider the quadratic function f(x) = x2 −4x−4, which can be written
in vertex
form
f(x) = (x − 2)2 − 8.
This is a parabola that opens upward. It is shifted to the right 2 units, then
downward
8 units. Therefore, it will cross the x-axis in two locations. Hence, one would
expect
that the quadratic formula would provide two real solutions (x-intercepts).
Indeed,
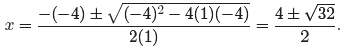
Note that the discriminant, D = 32 as calculated above, is
the number under the square
root. These solutions have approximations
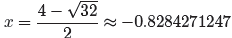 and
and 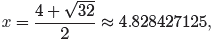
which aid in plotting an accurate graph of f(x) = (x − 2)2
− 8, as shown in
Figure 2.
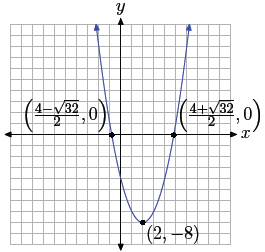
Figure 2. If the discriminant is positive,
there are two real x-intercepts.
Thus, if the discriminant is positive, the parabola will have two real
x-intercepts.
Next, let’s look at an example where the discriminant equals zero.
 Example 16. Consider again the quadratic
equation ax2 + bx + c = 0 and the
Example 16. Consider again the quadratic
equation ax2 + bx + c = 0 and the
solutions (zeros) provided by the quadratic formula
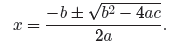
The expression under the radical, b2 −4ac, is
called the discriminant, which we denote
by the letter D. That is, the formula for the discriminant is given by
D = b2 − 4ac.
The discriminant is used to determine the nature and number of solutions to the
quadratic
equation ax2+bx+c = 0. This is done without actually calculating the
solutions.
Consider the quadratic equation
x2 − 4x + 4 = 0.
Calculate the discriminant and use it to determine the nature and number of the
solutions.
Compare x2 − 4x + 4 = 0 with ax2 + bx + c = 0 and note
that a = 1, b = −4, and
c = 4. The discriminant is given by the calculation
D = b2 − 4ac = (−4)2 − 4(1)(4) = 0.
Note that the discriminant equals zero.
Consider the quadratic function f(x) = x2 −4x+4, which can be written
in vertex
form
f(x) = (x − 2)2. (17)
This is a parabola that opens upward and is shifted 2 units to the right. Note
that
there is no vertical shift, so the vertex of the parabola will rest on the
x-axis, as shown
in Figure 3. In this case, we found it necessary to plot two points to
the right of the
axis of symmetry, then mirror them across the axis of symmetry, in order to get
an
accurate plot of the parabola.
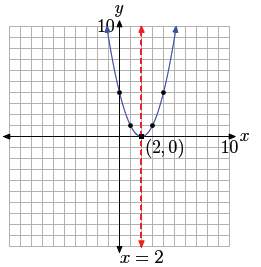
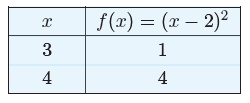
Figure 3. At the right is a table of points satisfying
f(x) = (x−2)2. These
points and their mirror images are seen as solid dots superimposed on the
graph of f(x) = (x − 2)2 at the left.
Take a closer look at equation (17). If we set f(x) = 0 in this equation,
then we
get 0 = (x − 2)2. This could be written 0 = (x − 2)(x − 2) and we
could say that the
solutions are 2 and 2 again. However, mathematicians prefer to say that “2 is a
solution
of multiplicity 2” or “2 is a double solution.”Note how the parabola is tangent
to
the x-axis at the location of the “double solution.” That is, the parabola comes
down
from positive infinity, touches (but does not cross) the x-axis at x = 2, then
rises again
to positive infinity. Of course, the situation would be reversed in the parabola
opened
downward, as in g(x) = −(x − 2)2, but the graph would still “kiss”
the x-axis at the
location of the “double solution.”
Still, the key thing to note here is the fact that the discriminant D = 0 and
the
parabola has only one x-intercept. That is, the equation x2 − 4x + 4
= 0 has a single
real solution.
Next, let’s look what happens when the discriminant is negative.
 Example 18. Consider the quadratic equation
Example 18. Consider the quadratic equation
x2 − 4x + 8 = 0.
Calculate the discriminant and use it to determine the nature and number of the
solutions.
Compare x2 − 4x + 8 = 0 with ax2 + bx + c = 0 and note
that a = 1, b = −4, and
c = 8. The discriminant is given by the calculation
D = b2 − 4ac = (−4)2 − 4(1)(8) = −16.
Note that the discriminant is negative.
Consider the quadratic function f(x) = x2 −4x+8, which can be written
in vertex
form
f(x) = (x − 2)2 + 4.
This is a parabola that opens upward. Moreover, it has to be shifted 2 units to
the right
and 4 units upward, so there can be no x-intercepts, as shown in Figure 4.
Again,
we found it necessary in this example to plot two points to the right of the
axis of
symmetry, then mirror them, in order to get an accurate plot of the parabola.
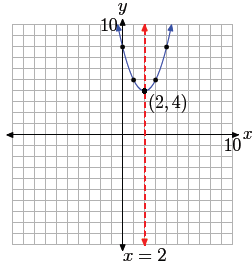
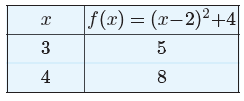
Figure 4. At the right is a table of points satisfying
f(x) = (x − 2)2 + 4.
These points and their mirror images are seen as solid dots superimposed on
the graph of f(x) = (x − 2)2 + 4 at the left.
Once again, the key point in this example is the fact that the discriminant is
negative
and there are no real solutions of the quadratic equation (equivalently, there
are no
x-intercepts). Let’s see what happens if we actually try to find the solutions
of x2 −
4x + 8 = 0 using the quadratic formula. Again, a = 1, b = −4, and c = 8, so
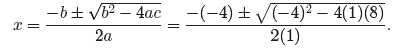
Simplifying ,
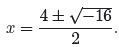
Again, remember that the number under the square root is the discriminant . In
this
case the disriminant is −16. It is not possible to square a real number and get
−16.
Thus, the quadratic equation x2 − 4x + 8 = 0 has no real solutions,
as predicted.
Let’s summarize the findings in our last three examples.
ax2 + bx + c = 0.
The discriminant is
defined as
D = b2 − 4ac.
There are three possibilities:
1. If D > 0, then the quadratic equation has two real solutions.
2. If D = 0, then the quadratic equation has one real solution.
3. If D < 0, then the quadratic equation has no real solutions.
This key result is reflected in the graph of the quadratic function.
f(x) = ax2 + bx + c.
The graph of
this function is a parabola. Three possibilities exist depending upon
the value of the discriminant D = b2 − 4ac.
1. If D > 0, the parabola has two x-intercepts.
2. If D = 0, the parabola has exactly one x-intercept.
3. If D < 0, the parabola has no x-intercepts.
| Prev | Next |