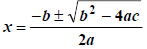Completing the Square and the Quadratic Formula
(1) We now have three of the five methods for solving quadratic equations – can
you name and demonstrate each of them? We’ll now take on the task of learning
the last two methods .
(2) The first of these relies on observing how simple it was to solve quadratic
equations of the form (x-4)2=7 by using the Perfect Square Rule. The left side
of this equation is the square of a binomial difference and would look like
x2-8x+16 if expanded. We would recognize this as a perfect square trinomial
based on the hundreds of factoring problems we’ve done. So, had the equation
been given as x2-8x+16 =7 , we could factor the left side and get (x-4)2=7 and
then use the Perfect Square Rule. But what if we were given x2-8x+9=0 ? The
observant student should see how I got this – subtract 7 from both sides of
x2-8x+16 =7 . Our quest is to do the reverse of this – start with
x2-8x+9=0 and discover how to manipulate it into a perfect square trinomial
equaling a number.
(3) The method is called completing the square, and it relies on understanding
the form of a perfect square trinomial a bit better:
(x+a)2=x2+2ax+a2
Notice the linear coefficient, 2a. Taking one half of it,
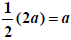 , gives the object which is added to x in the
binomial , x+a, and whose square, a2, appears as the constant in the trinomial.
So that is how perfect square trinomials are formed: the constant is the square
of1/2 of the linear coefficient .
, gives the object which is added to x in the
binomial , x+a, and whose square, a2, appears as the constant in the trinomial.
So that is how perfect square trinomials are formed: the constant is the square
of1/2 of the linear coefficient .
(4) We use the above concept to create a perfect square trinomial by the
technique called completing the square.
Example 1: Solve x2+6x-2 = 0
Solution: In order to create the proper constant to have this be a perfect
square trinomial , we first make room for it by, in this case, adding 2 to both
sides.
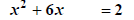 |
Make room for new constant |
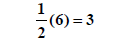 |
Take 1/2 the linear coefficient The square of is the constant we need to make a perfect square trinomial, x2 + 6x + 9 But we can't just add to one side, we have to add it to BOTH side |
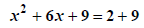 |
Simplify |
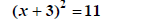 |
Use Perfect Square Rule |
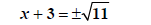 |
Subtract 3 from both sides |
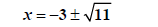 |
Example 2: Solve x2-5x+3=0
Solution:
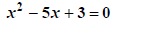 |
Make room for new constant |
 |
Take half the linear coefficient |
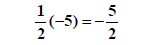 |
The square of this is the new constant which we add to BOTH sides |
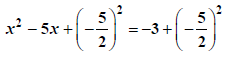 |
|
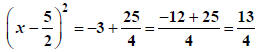 |
Use Perfect Square Rule |
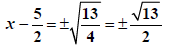 |
Add 5/2 to both sides |
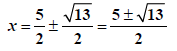 |
(5) ZZZZZ This method ONLY WORKS ON MONIC QUADRATICS –
i.e., where the leading coefficient is 1. If it isn’t 1 in what you start with,
then you must divide both sides of the equation by the leading coefficient to
make monic.
Example 3: Solve 4x2-8x-3=0
Solution:
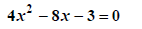 |
Make monic by dividing by 4 |
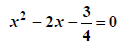 |
Create constant space |
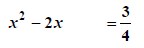 |
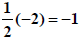 , , whose square is added to BOTH sides |
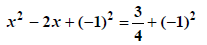 |
|
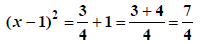 |
Use Perfect Square Rule |
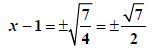 |
Add 1 to both sides |
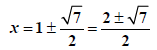 |
(6) We can apply this method to an arbitrary quadratic equation in standard
form. The end result is a formula for x in terms of the coefficients a, b and c.
It is known as the Quadratic Formula .
(7) Let’s concentrate a bit on the a, b and c in the standard form of the quadratic equation.
ax2+bx+c=0
a is the coefficient of the quadratic term,
b is the coefficient of the linear term, and
c is the constant (object with no x in it).
This statement highlights something more than just the definitions of a, b and
c. It says there can be ONLY ONE term containing x2, there can be ONLY ONE term
containing x, and the constant is the entire collection of terms which do not
contain x. For example, consider mx2+4x=3-mx. This is quadratic in x so we
create an equation to 0: mx2+4x+mx-3=0. This is NOT in standard form since
there are two linear terms, 4x and mx. We can ONLY have ONE linear term in order
to use the Quadratic Formula, so we create a single linear term by distributing
an x out of these two terms: mx2+(4+m)x-3=0 . Now we can identify a,
b and c: a=m,b=4+m,and c=-3. Thus, we have
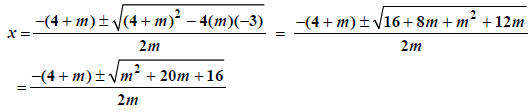
Here’s another example: Solve for x in (x-1)2+y2=4x. Notice first that we
can’t isolate the (x-1)2 as 4x-y2 and use the Perfect Square Rule since this
would place an x in the answer to a problem where we want to solve for . So we
go back to basics and multiply it out:
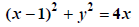 |
Remove grouping symbols |
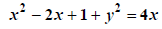 |
Quadratic in x=> try for standard form |
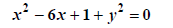 |
OK:a=1,b= -6,c=1+y2 |
| That's right, remember is made up of all terms not containing x |
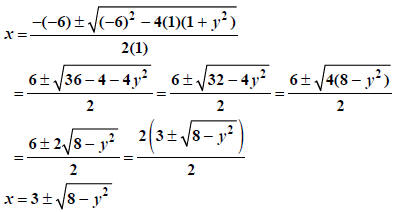
| Prev | Next |