Math 1051 Precalculus I Lecture Notes

5.1 Composite Functions

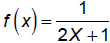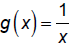Given AND find (f ο g)(x)

 

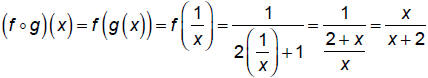
Domain f:	Domain g:	Domain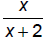
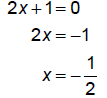	x ≠ 0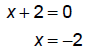
So	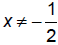x ≠ 0	x ≠ -2

Domain of (f ο g)(x) must respect domains of g and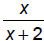. So, we get {x | x ≠ 0, x ≠ -2}
Domain of a composite function

5.2 One-to-One Functions & Inverse Functions

Determine whether a function is one-to-one
Use horizontal line test on the graph of a given function.
Inverse of a function by mapping
Graph of the inverse of a function
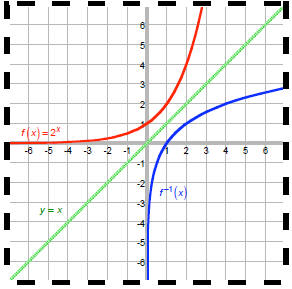
The function and its inverse are symmetric about the line y = x.

Inverse of a function given its equation

pg 261, #68: Find the inverse of


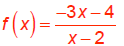
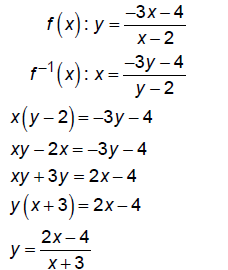
So, the inverse function is

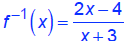
Domain of f: {x | x ≠ 2}
Range of f = Domain of f inverse: {y | y ≠ -3}
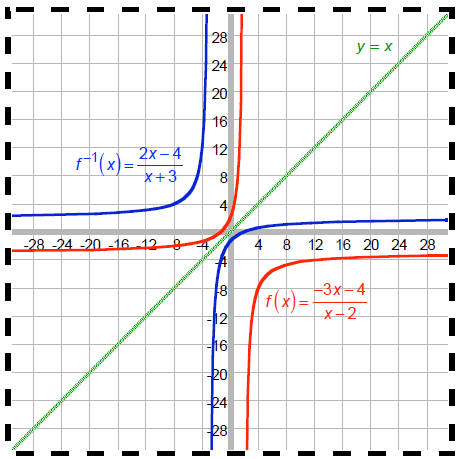
Here is the graph. Note the symmetry of the function and its inverse about the line y = x .

5.3 Exponential Functions

Definition
f (x) = a^x a > 0, a ≠ 1

Graph exponential functions
Define the number e

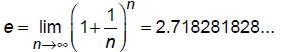
Solve exponential equations

pg 274 #70: Solve

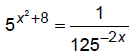
We can write the exponential functions with the same base and then equate the exponents:

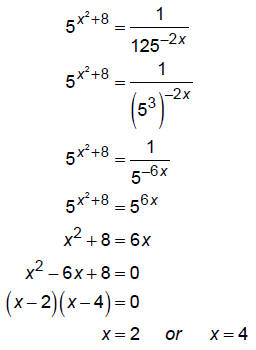
These are both in the domain of the original equation.
Or, if we could not write the expressions with the same bases, we would use logs:

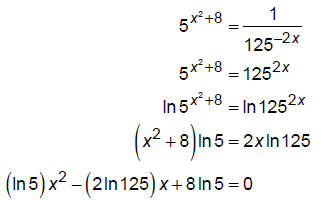
Now, we can use the quadratic formula to solve this:

So, we get the same answer as before.

5.4 Logarithmic Functions

Change between log and exponential forms

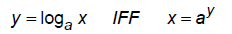
Evaluate logarithmic expressions
Domain
Graph logarithmic functions

5.5 Properties of Logarithms

Properties
Memorize the properties
Function operating on its inverse: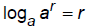
Function operating on its inverse: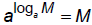
Log of a product : log_aMN = log_aM + log_aN
Log of a quotient: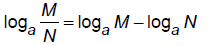
Log of a power :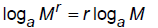
Equal exponentials: If a^M = a^N then M = N ,
M, N, and a are positive real numbers, a ≠ 1

Equal logs: If log_aM = log_aN then M = N ,
M, N, and a are positive real numbers , a ≠ 1

Rewrite logarithmic expressions using properties
Change-of-base formula

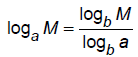
5.6 Logarithmic and Exponential Equations

Solve logarithmic equations
pg 303 #24: Solve log₅(x + 3) = 1- log₅(x -1).
Put all logs together on one side of equation and then change to exponential:

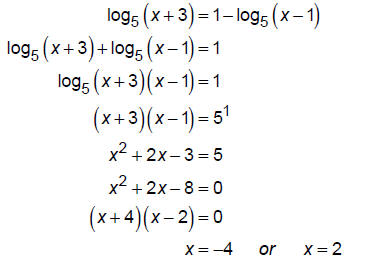
-4 is not in the domain of the original equation so the only solution is x = 2.

Solve exponential equations
Solve: 81^x + 2 = 3 • 9^x
Can we make the bases of the exponentials the same?

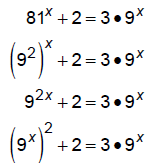
Now, we have 9^x and 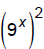so try a u substitution :

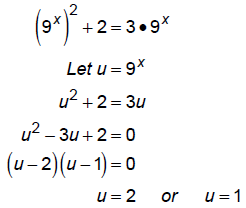
Now, back substitute:

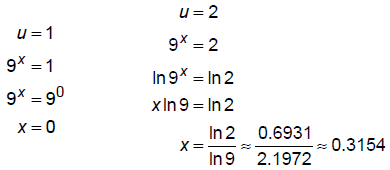
5.7 Compound Interest

Determine future value of a lump sum of money
Calculate effective rates of return
Determine present value of a lump sum of money

Memorize the formulas.
Simple interest : I = Prt

Compound interest:

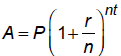
Continuous compounding: A = Pe^rt
Effective rate of interest:
I_simple= I_compound