Math 1051 Precalculus I Lecture Notes
4.1 Polynomial Functions and Models
Degree
Power functions
Graph polynomial functions using transformations
Identify real zeros of polynomial functions and their
multiplicities
Behavior near a zero
Turning points
End behavior
Analyze the graph of a polynomial function



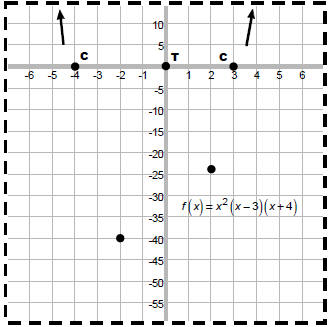
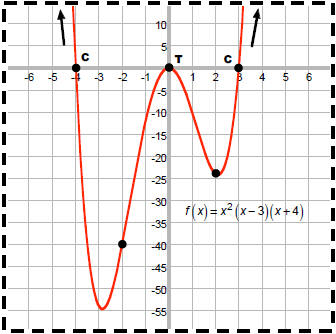
pg 182 #78: Graph f (x) = x2(x - 3)(x + 4)

y-intercept:
f (x) = x2(x - 3)(x + 4)
f (x) = 02(0 - 3)(0 + 4)
= 0
x-intercepts:
f (x) = x2 (x - 3)(x + 4)
0 = x2 (x - 3)(x + 4)
x = 0,multiplicity 2,which is even so graph TOUCHES x - axis here
x = 3,multiplicity 1,which is odd so graph CROSSES x - axis here
x = -4,multiplicity 1,which is odd so graph CROSSES x - axis here
End behavior: graph looks like
f (x) = axn .
As | x | →∞ , f (x) → x4 , which looks like y = x4 .
Max number of turning points = n - 1 = 4 - 1 = 3.
Plot some specific points if necessary:
f (-2) = (-2)2(-2 - 3)(-2 + 4) = 4 • (–5) • 2 = -40
f (2) = (2)2(2 - 3)(2 + 4) = 4 • (–1) • 6 = -24
 -5
-5
4.2 Properties of Rational Functions
Domain
Vertical asymptotes

Multiplicity of vert asym shows behavior near asym.
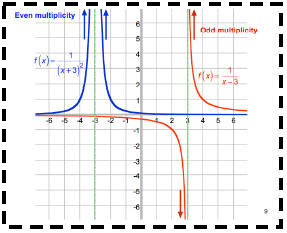
For the vertical asymptote, remember that
• If the multiplicity is ODD, as the graph
approaches the asymptote from different
directions, ONE SIDE will go to positive
infinity and the OTHER to negative
infinity.
Think of the graph of
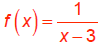
• If the multiplicity is EVEN, as the graph
approaches the asymptote from different
directions, BOTH sides will go to positive
infinity or BOTH sides will go to negative
infinity.
Think of the graph of
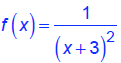
Horizontal or oblique asymptotes
4.3 Graph of a Rational Function
Analyze the graph of a rational function, including holes.


pg 207, #28: Graph
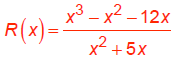
1. Factor:
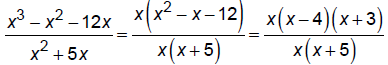
Domain:{x | x ≠ 0, x ≠ -5}
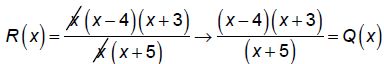
Since the x's cancel, there will be a hole at x = 0.
To find the y- value of the hole , find
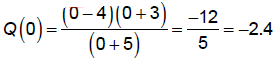
2. Intercepts
x-intercepts:
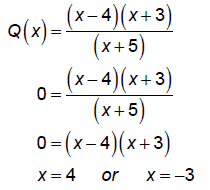
x = 4 has multiplicity 1, which is odd, so graph CROSSES here
x = -3 has multiplicity 1, which is odd, so graph CROSSES here
y-intercept
This is R(0) but 0 is not in the domain so there is no y-intercept.
3. Vertical asymptotes: x = -5
For the vertical asymptote, remember that
• If the multiplicity is ODD, as the graph approaches the asymptote from
different directions , ONE
SIDE will go to positive infinity and the OTHER to negative infinity .
Think of the graph of
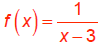
• If the multiplicity is EVEN, as the graph approaches the asymptote from
different directions,
BOTH sides will go to positive infinity or BOTH sides will go to negative
infinity.
Think of the graph of
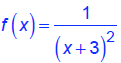
The multiplicity of x = -5 is odd, so near –5 the graph will go up on one side
and down on the
other.
4. Horizontal or oblique asymptotes:
Since the degree of the numerator is exactly 1 more than the
degree of the denominator, there is an oblique asymptote. Use
long division to find it .
OA is y = x - 6
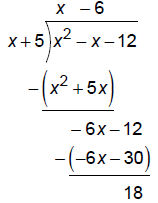
5. Plot where graph crosses HA or OA by solving
Function = Asymptote
R(x) = y
Does R cross the oblique asymptote?
Function = oblique asymptote
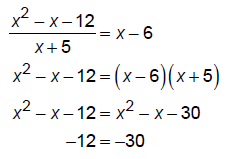
This has no solution so the graph does not cross the oblique asymptote.
6. Plot a point or two to help with the sketch.
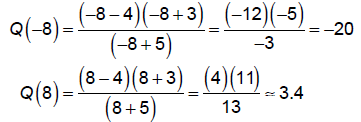
Now, plot the intercepts , draw the asymptotes, and sketch the graph.
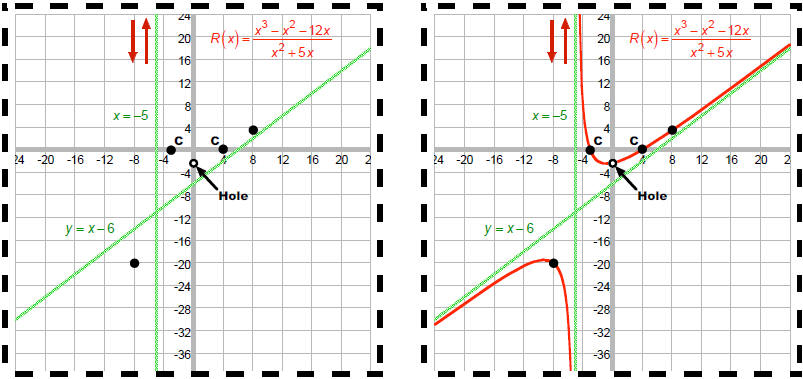
Applications of rational functions
Word problems - set these up like we did previous ones .
4.4 Polynomial and Rational Inequalities
Solve polynomial inequalities
Solve rational inequalities

pg 214, #36: Solve:
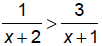
Put everything on one side and zero on the other and figure out the signs:
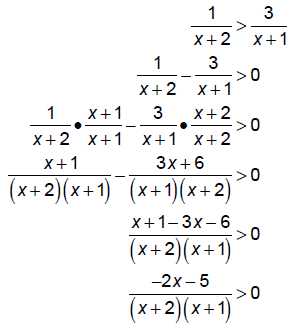
The zeros of all the factors are :
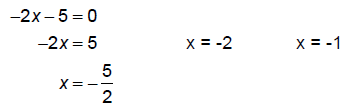
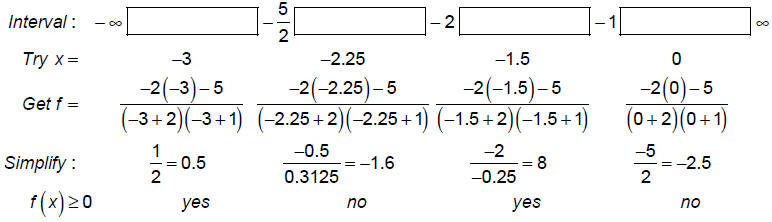
So, the solution is
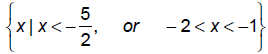
| Prev | Next |