Math 110 Exam 2
Fall 2007
1. Your exam contains 7 questions and 5 pages; Please make sure you have a
complete exam.
2. The entire exam is worth 50 points. Point values for problems vary and these
are clearly
indicated. You have 50 minutes for this exam.
3. Make sure to ALWAYS SHOW YOUR WORK; you will not receive any partial credit
unless
all work is clearly shown. If in doubt, ask for clarification.
4. If you need extra space, use the back of the page and clearly indicate this.
5. You are allowed one 8.5×11 sheet of handwritten notes (both sides). Graphing
and scientific
calculators are allowed .
| Problem | Total Points | Score |
| 1 | 12 | |
| 2 | 6 | |
| 3 | 5 | |
| 4 | 6 | |
| 5 | 5 | |
| 6 | 4 | |
| 7 | 12 | |
| Total | 50 |
1. (4 points each) Let f(x) = 3x2−5x and g(x) =
x−2. Find the following. Simplify (when
applicable).
(a) (fg)(1)
(b) (f − g)(x)
(c) (f g)(x)
2. (3 points each) Let f(x) be the function given by the table

(a) Find 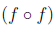 (0)
(0)
(b) Find f−1(−2).
3. (5 points) Find all zeros of the polynomial P(x) = x3−
6x2 + 9x. State the multiplicity
of each zero .
4. (6 points) Divide P (x) = 2x3− x2
− 7x + 2 by D(x) = x2− 2x − 1. Express your answer
in the form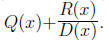
5. (5 points) Use synthetic division and the Remainder
Theorem to find P(−3) if P(x) =
2x4 + 5x3− 4x2 + 5.
6. (4 points) List all possible rational zeros of P(x) =
2x3−5x2+x+6 given by the Rational
Zeros Theorem (but don’t bother checking which are actually zeros).
7. (6 points each) Let r(x) =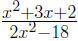 .
.
(a) Find the x- and y- intercepts of r (x).
(b) Find all asymptotes of r(x). (You do not need to draw the graph .)
| Prev | Next |