MATH HOMEWORK 04
Exercise 4.1. Answer the following questions.
• What is a rational number ?
• Which fraction is called proper? Which fraction is called improper?
Give two examples of proper fractions and two examples of improper
fractions. Explain.
• Which number is called a mixed number? Give two examples of a
mixed number.
• What is a decimal number ? What is a terminating decimal number?
What is a repeating decimal number ?
Exercise 4.2. Reduce the following fraction to its
lowest terms. Determine
whether this number is proper fraction or not . If not, present it as a mixed
number.
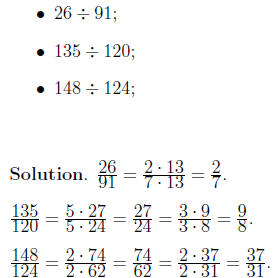
Exercise 4.3. Present each decimal number as a
ratio of two integers. DO
NOT reduce the fraction into lowest terms.
• 0.2345, 0.452 (terminating)
• 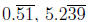 (repeating)
(repeating)
Solution .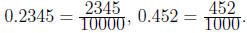
Let 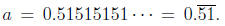 We multiply this
number by 10, 100,
We multiply this
number by 10, 100,
1000, etc. until we see how to get rid of the repeating part.
We get 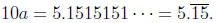
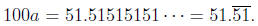 We see that 100a and a
have the same
We see that 100a and a
have the same
digits after the decimal point. Then,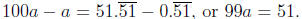
Therefore,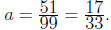
Let 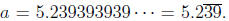 Then,
Then,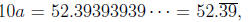
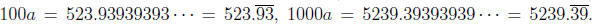
We can see that the numbers 10a and 1000a have the same digits after the
decimal point. Therefore,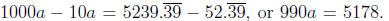 Thus,
Thus,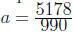
Exercise 4.4. Evaluate the expression. Explain each step.
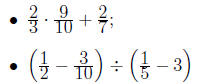
Exercise 4.5. To repair his sprinkler system, Tony
Gambino needs a total
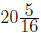 inches of PVC pipe. He has on hand pieces
that measure
inches of PVC pipe. He has on hand pieces
that measure 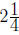 4 inches,
4 inches,
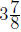
inches, and 1/4 inches in length. If he can combine these pieces and use them
in the repair, how long of piece of PVC pipe will Tony need to purchase to
repair his sprinkler system ?
Solution . First, we compute how much pipe is
possessed by Tony Gambino.
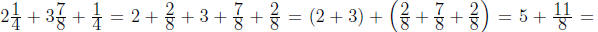
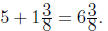 So, he already has 638 inches of the pipe.
So, he already has 638 inches of the pipe.
Second, we compute how much of the additional pipe he
needs to buy.
We get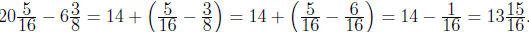
Therefore, he needs to buy additional 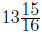 inches
of PVC pipe.
inches
of PVC pipe.
Exercise 4.6. What is the perfect square? Write
down all perfect squares
less than 200.
Solution.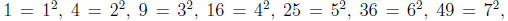
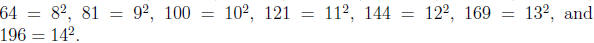
Exercise 4.7. Evaluate
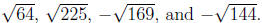
Solution. Fsing the results from Exercise 4.6, we
get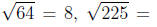
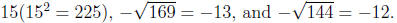
Exercise 4.8. Simplify the radicals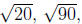 and
and
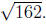
Solution.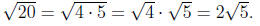
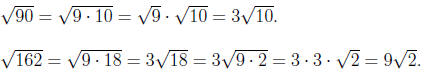
Exercise 4.9. Perform the indicated operation.
Simplify the answer when
possible.
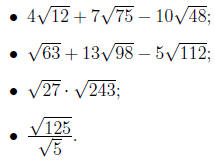
Solution. First, we simplify all square roots:
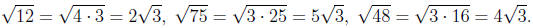
Second, we gather all terms :
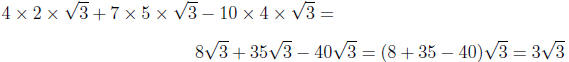
Exercise 4.10. Rationalize the denominator.
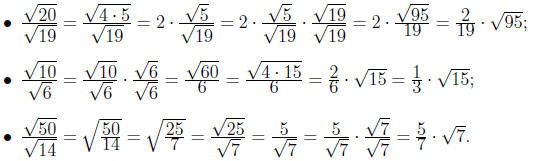
| Prev | Next |