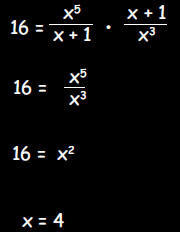Answer Key for California State Standards: Algebra I
| 7.0: Students verify that a point lies on a line, given an
equation of the line. Students are able to derive linear equations by using the point-slope formula. |
a. Write an equation involving only numbers that shows
that the point 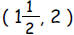
lies on the graph of the equation 2y = 6x - 5.

b. A line has a slope of
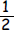 and passes through the point (5, 8).
and passes through the point (5, 8).
What is the equation for the line?
The equation of the line must be of the form y = mx + b. The slope
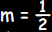 is isgiven. Therefore, 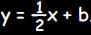 . To find the y
intercept b , substitute the . To find the y
intercept b , substitute thecoordinates of the point (5,8) for x and y in the equation 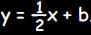 . This gives: . This gives:
Therefore This result may also be obtained by using the
point-slope formula for a |
| 8.0: Students understand the concepts of parallel lines
and perpendicular lines and how those slopes are related. Students are able to find the equation of a line perpendicular to a given line that passes through a given point. |
a. A line is parallel to the line for the equation:
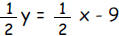 . What is the slope of the parallel line?
. What is the slope of the parallel line?
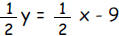 may be rewritten as y = x - 18,
which has slope 1. may be rewritten as y = x - 18,
which has slope 1.Any line parallel to this one must have the same slope, 1. |
b. What is the slope of a line perpendicular to the line
for the
equation 3y = 7 - 6x ?
3y = 7 - 6x may be rewritten as 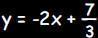 . The
slope m of any line . The
slope m of any lineperpendicular to this one must satisfy m(-2) = -1. Therefore |
c. What is the equation of a line passing through the
point ( 7, 4 ) and
perpendicular to the line having the equation 3x - 4y - 12 = 0?
The equation 3x - 4y - 12 = 0 may be rewritten as
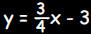 . The slope of this line . The slope of this lineis 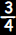 . The slope m of any line
perpendicular to this one must satisfy . The slope m of any line
perpendicular to this one must satisfy
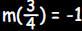 . .Therefore 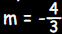 . So the equation of any perpendicular line must be of
the form . So the equation of any perpendicular line must be of
the form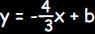 . Since the graph of the line
contains the point (7,4), it is also true that . Since the graph of the line
contains the point (7,4), it is also true that
So the answer is
|
| 9.0: Students solve a system of two linear equations in
two variables algebraically and are able to interpret the answer graphically. Students are able to solve a system of two linear inequalities in two variables and to sketch the solution sets. |
a. Solve for the numbers x and y from the equations 2x - y = 1 and 3x - 2y = -1
There are other ways to solve this problem. One
can use one of the 3x - 2(2x - 1) = -1 |
b. Graph the equations 2x - y = 1 and 3x - 2y = -1 and
circle the portion
of the graph which corresponds to the solution to the above
problem on your graph.
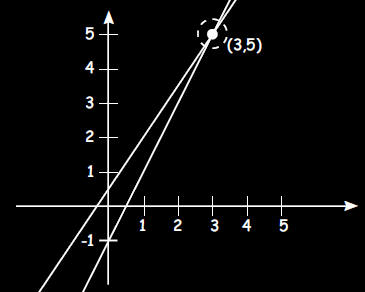
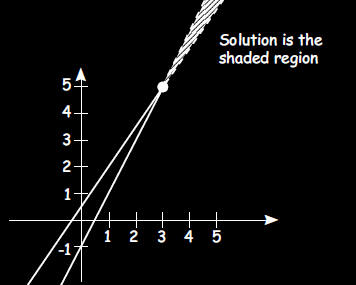
c. Graph the solution to the linear inequalities
2x - y > 1 and 3x - 2y < -1
| 10.0: Students add, subtract , multiply, and divide
monomials and polynomials . Students solve multistep problems, including word problems, by using these techniques. |
a. Simplify
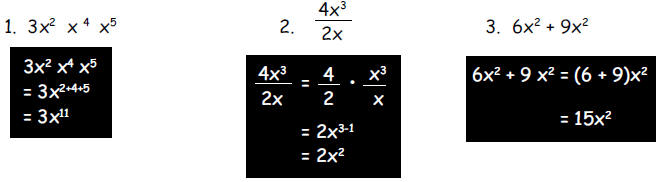
b. Let P = 2x2 + 3x - 1 and Q = -3x2 + 4x - 1
1. Calculate P + Q and collect like terms.
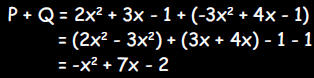
2. Calculate P - Q and collect like terms.
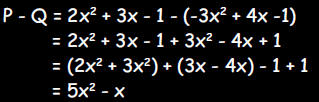
c. Calculate the product ( x2 - 1 ) ( 2x2 - x - 3 ) and collect like terms.
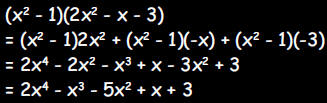
d. The area of a rectangle is 16. The length of the
rectangle is 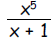
and the width is 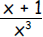 . What is x?
. What is x?
|
A = length times width
|
| Prev | Next |
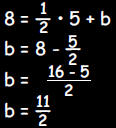
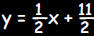
 and substituting
and substituting
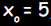 , and
, and
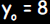 .
.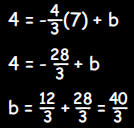
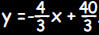 . This answer may also be obtained by
using the
. This answer may also be obtained by
using the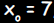 , and
, and
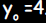 .
.