Primes and Greatest Common Divisors

Primes

Definition:A positive integer p greater than 1 is called primeis the only positive factors of p are 1 and p.

Definition: A positive integer that is greater than 1 and is not prime is called composite.
Primes less than 100 are:
2, 3, 5, 7, 11, 13, 17, 19, 23, 29, 31, 37, 41, 43,
47, 53, 59, 61, 67, 71, 73, 79, 83, 89, 97.

The fundamental Theorem of Arithmetic

Theorem:Every positive integer greater than 1 can
be written uniquely as a prime or as the product of
two or more primes where the prime factors are
written in order of nondecreasingsize .

Examples:
100= 2². 5²
641=641
999= 3³. 37
1024= 2¹0

A procedure for showing that an integer is prime:

Theorem: If n is a composite integer, then n has
a prime divisor less than or equal to .

Example:Show 101 is prime.
Solution : The only primes not exceeding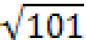
are 2, 3, 5, 7. Because 101 is not divisible by 2, 3, 5,
or 7 (the only quotient of 101 and each of these
integers is not an integer), it follows that 101 is
prime.

Theorem:There are infinitely many primes!

There is an ongoing quest to discover larger and
larger prime numbers; for almost all the last 300
years, the largest prime known has been an
integer of the special form 2^p–1, where p is
also prime. Such primes are called Mersenne
primes.

Example: 2²-1 = 3, 2³-1 = 7, 2⁵-1 =31are Mersenneprimes, while 2¹¹-1 = 2047 is not a Mersenneprime because 2047= 23.89.

Conjectures and Open Problems About Primes

Large prime numbers have many applications in
cryptology.
It would be useful to have a function f(n) such
that f(n) is prime for all positive integers n.
After a lot of computation we may encounter
the polynomial f (n) = n²–n + 41. This polynomial
has interesting property that f (n) is prime for n
integer number between 0 < n < 41.

Conjecture: f(n) = n²–n + 41 is prime for all integer? NO

f(1)=41
f(2)= 43
f(3)= 47
f(4)=53
BUT
f(41)= 41²-41 +41 = 41² NOT a PRIME!

Goldbach’sConjecture

In 1742 Goldbachin a letter to Euler conjectured that every odd integer n, n>5, is the sum of three primes. Euler replied the conjecture is equivalent to the conjecture that every even integer n, n>2, is the sum of two primes.
4=2+2, 6=3+3, 8 = 5+3, 10 = 7+3, 12 = 7+5
As of 2006 the conjecture has been checked for all positive even integer up to 2. 10¹⁷

Greatest common Divisors and Least Common Multiple

Definition: Let a and b be integers, not both zero.
The largest integer d such that d|aand d|bis called
the greatest common divisor of a and b. The
greatest common divisor of a and b is denoted by
gcd(a,b).

Example:What is the greatest common divisor of
24 and 36?
Solution: The positive common divisors of 24 and
36 are 1, 2, 3, 4, 6, 12. Hence gcd(24,36)=12.

Relatively Prime

Definition: The integers a and b are relatively
primeif their greatest common divisor is 1.
i.e. gcd(a,b)=1.

Example: gcd(17, 22) =1 therefore 17 and 22 are relatively prime.

The Least Common multiple

The least common multiple of the positive
integers a and b is the smallest positive integer
that is divisible by both a and b.
The least common multiple of a and b is
denoted by lcm (a, b).

Example:
lcm(2³3⁵7², 2⁴3³)=2^max(3,4)3^max(3,5)7^max(2,0)= 2⁴3⁵7²