Quadratic Functions
| Zeros of Quadratic Functions In this page we define what is meant by a zero of a quadratic function and how to find all of them. By a zero of a quadratic function 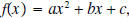 we mean a number x 0
such that we mean a number x 0
such that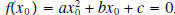 |
||||||
| There are two ways to find the zeros of a
quadratic function. The first, and easiest, is to factor the quadratic expression if you can . The second, and this always works, is to use the quadratic formula. Recall, if the expression 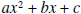 equals zero, then equals zero, then
|
||||||
Example 1: Find the zeros of
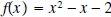 by factoring. by factoring.Solution: The integer factors of -2 are 1 and 2 with one of them being negative. So we try 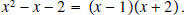 (Not correct) (Not correct)However, when we multiply the two factors together to see if we’ve got it correct, we compute 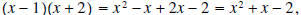 which is not what we want. The coefficient of x is off by a minus sign. So we try 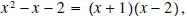 and this is correct. The zeros of 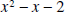 are the solutions of the following equation
are the solutions of the following equation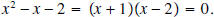 The only way a product can equal zero is for one of the factors to equal zero. Thus, we have 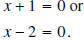 From which we conclude that 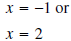 Notice that there are exactly two zeros. |
||||||
Example 2: What are the zeros of
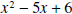 ? ?Solution: 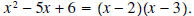 Thus the zeros of this
quadratic function are Thus the zeros of this
quadratic function are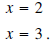 |
||||||
Example 3: Find the zeros of
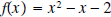 by using the quadratic formula. by using the quadratic formula.Solution: We are looking to find those x for which 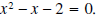 The solutions of this equation are The solutions of this equation aregiven by the quadratic formula 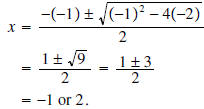 |
||||||
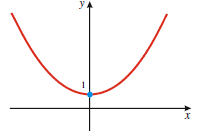
We now discuss why some quadratic functions have
no zeros. If we graph the quadratic function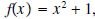 we see that it never crosses the
x-axis. This means that f x never equals zero, or this function we see that it never crosses the
x-axis. This means that f x never equals zero, or this functionhas no zeros.
It is instructive to use the quadratic formula to
find the zeros of
Since we cannot take the square root of a negative
number and get a real number, we see that there is no real |
||||||
Example 4: Does
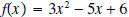 have any zeros? have any zeros?Solution: Using the quadratic formula to solve the equation 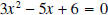 we have : we have :
Since negative numbers do not have real square roots, this quadratic function has no zeros. |
||||||
| In the table below we summarize the possibilities
of zeros for an arbitrary quadratic function
Definition: The expression
|
||||||
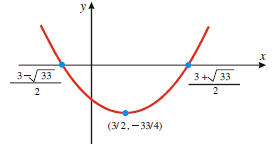
Example 5: Calculate the discriminate of
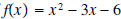 and plot the function . and plot the function .Solution:
Since the discriminate is positive we know that
|
||||||
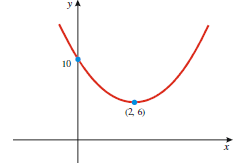
Example 6: Calculate the discriminate of
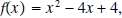 and plot the function. and plot the function.Solution: 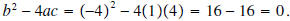 Since the discriminate is zero, there is only one zero, and it equals 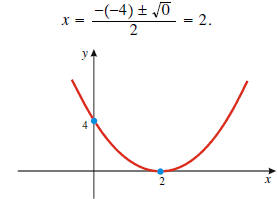 |
||||||
Example 7: Calculate the discriminate of
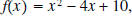 and plot the function. and plot the function.Solution: 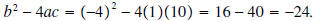 Since the discriminate is negative, this quadratic function has no zeros.
|
| Prev | Next |
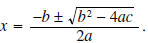
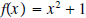 .
.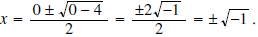
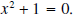 That is
That is
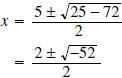
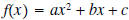
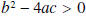
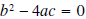
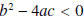
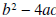 is called the
discriminate of the function
is called the
discriminate of the function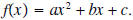
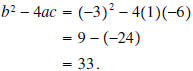
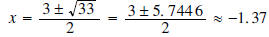 and 4.37
and 4.37