Note: The sample
problems illustrate
the standards and
are written to help
clarify them. Some
problems are written
in a form that can be
used directly with
students; others will
need to be modified,
particularly in the
primary grades,
before they are
used with students.The symbol

identifies the key
standards for
grade seven.
|
Number Sense
1.0 Students know the properties of, and compute with, rational numbers
expressed in a variety of forms:
1.1 Read, write, and compare rational numbers in
scientific notation (positive
and negative powers of 10) with approximate numbers using scientific
notation.
Write the following as a power of 10 or the product of a whole number
and a power of 10:
1. 10,000
2. Ten billion
3. 6,000,000
4. 3 hundred thousand
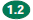 Add, subtract,
multiply, and divide rational numbers (integers, fractions, and Add, subtract,
multiply, and divide rational numbers (integers, fractions, and
terminating decimals) and take positive rational numbers to whole-number
powers.
Write the prime factorization of the following
numbers:

1.3 Convert fractions to decimals and percents and
use these representations in
estimations, computations, and applications.
Change to decimals:
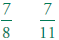
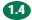 Differentiate
between rational and irrational numbers. Differentiate
between rational and irrational numbers.
 Know that
every rational number is either a terminating or repeating decimal Know that
every rational number is either a terminating or repeating decimal
and be able to convert terminating decimals into reduced fractions .
Change to fractions:
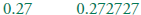
Find the period of the repeating part of
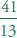 . .
1.6 Calculate the percentage of increases and
decreases of a quantity.
 Solve problems
that involve discounts, markups, commissions, and profit Solve problems
that involve discounts, markups, commissions, and profit
and compute simple and compound interest.
Joe borrows $800 at 10% interest compounded
every six months. How
much interest will there be in 4 years?
2.0 Students use exponents, powers, and roots and use exponents in
working
with fractions:
2.1 Understand negative whole-number exponents. Multiply and divide
expressions involving exponents with a common base.
Continue the sequence:
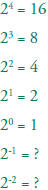
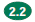 Add and
subtract fractions by using factoring to find common denominators. Add and
subtract fractions by using factoring to find common denominators.
Make use of prime factors to compute:
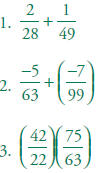
 Multiply,
divide, and simplify rational numbers by using exponent rules. Multiply,
divide, and simplify rational numbers by using exponent rules.
2.4 Use the inverse relationship between raising
to a power and extracting the
root of a perfect square integer; for an integer that is not square,
determine
without a calculator the two integers between which its square root lies
and
explain why.
Find the edge of a square which has an area of
81.
 Understand the
meaning of the absolute value of a number; interpret the Understand the
meaning of the absolute value of a number; interpret the
absolute value as the distance of the number from zero on a number line;
and determine the absolute value of real numbers.
|
|
| |
Algebra and Functions1.0 Students
express quantitative relationships by using algebraic terminology,
expressions, equations, inequalities, and graphs:
1.1 Use variables and appropriate operations to write an expression, an
equation,
an inequality, or a system of equations or inequalities that represents
a verbal
description (e.g., three less than a number, half as large as area A).
Write the following verbal statements as algebraic expressions:
1. The square of a is increased by the sum of twice a and 3.
2. The product of 1⁄2 of a and 3 is decreased by the quotient of a
divided by
(-4).
1.2 Use the correct order of operations to evaluate algebraic
expressions such as
3(2x + 5)2.
Given x = (-2) and y = 5 evaluate:
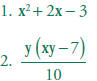
 Simplify
numerical expressions by applying properties of rational numbers Simplify
numerical expressions by applying properties of rational numbers
(e.g., identity, inverse, distributive, associative, commutative) and
justify the
process used.
Name the property illustrated by each of the
following:
1. x (y + -y) = x (0)
2. x (y + -y) = xy + x(-y)
3. x (y + -y) = (y + -y)(x)
4. x (y + -y) = x (-y + y)
5. x (y (1/y)) = x (1)
1.4 Use algebraic terminology (e.g., variable, equation, term,
coefficient ,
inequality, expression, constant) correctly.
1.5 Represent quantitative relationships graphically and interpret the
meaning
of a specific part of a graph in the situation represented by the graph.
2.0 Students interpret and evaluate expressions involving integer
powers and
simple roots:
2.1 Interpret positive whole-number powers as repeated multiplication
and
negative whole-number powers as repeated division or multiplication by
the multiplicative inverse. Simplify and evaluate expressions that
include
exponents.
2.2 Multiply and divide monomials; extend the process of taking powers
and
extracting roots to monomials when the latter results in a monomial with
an integer exponent.
3.0 Students graph and interpret linear and some nonlinear functions:
3.1 Graph functions of the form y = nx2 and y = nx3
and use in solving problems.
3.2 Plot the values from the volumes of three-dimensional shapes for
various
values of the edge lengths (e.g., cubes with varying edge lengths or a
triangle
prism with a fixed height and an equilateral triangle base of varying
lengths).
 Graph linear
functions, noting that the vertical change (change in y-value) Graph linear
functions, noting that the vertical change (change in y-value)
per unit of horizontal change (change in x-value) is always the same and
know that the ratio (“rise over run”) is called the slope of a graph.
 Plot the
values of quantities whose ratios are always the same (e.g., cost to Plot the
values of quantities whose ratios are always the same (e.g., cost to
the number of an item, feet to inches, circumference to diameter of a
circle).
Fit a line to the plot and understand that the slope of the line equals
the
quantities.
 Students
solve simple linear equations and inequalities over the rational Students
solve simple linear equations and inequalities over the rational
numbers:
 Solve
two- step linear equations and inequalities in one variable over the Solve
two- step linear equations and inequalities in one variable over the
rational numbers, interpret the solution or solutions in the context
from
which they arose, and verify the reasonableness of the results.
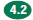 Solve
multistep problems involving rate, average speed, distance, and time Solve
multistep problems involving rate, average speed, distance, and time
or a direct variation.
|
|
| |
Measurement and Geometry
1.0 Students choose appropriate units of measure and use ratios to
convert within
and between measurement systems to solve problems:
1.1 Compare weights, capacities, geometric measures, times, and
temperatures
within and between measurement systems (e.g., miles per hour and feet
per
second, cubic inches to cubic centimeters).
Convert the following:
1. 80 miles/hr. = ? ft./sec.
2. 20 oz./min. = ? qts./day1.2
Construct and read drawings and models made to scale.
 Use measures
expressed as rates (e.g., speed, density) and measures expressed Use measures
expressed as rates (e.g., speed, density) and measures expressed
as products (e.g., person-days) to solve problems; check the units of
the
solutions; and use dimensional analysis to check the reasonableness of
the
answer.
2.0 Students compute the perimeter, area, and
volume of common geometric
objects and use the results to find measures of less common objects.
They
know how perimeter, area, and volume are affected by changes of scale:
2.1 Use formulas routinely for finding the perimeter and area of basic
two-dimensional figures and the surface area and volume of basic
three-dimensional
figures, including rectangles, parallelograms, trapezoids,
squares, triangles, circles, prisms, and cylinders.
2.2 Estimate and compute the area of more complex or irregular two- and
three-dimensional figures by breaking the figures down into more basic
geometric objects.
2.3 Compute the length of the perimeter, the
surface area of the faces, and the
volume of a three-dimensional object built from rectangular solids.
Understand
that when the lengths of all dimensions are multiplied by a scale
factor,
the surface area is multiplied by the square of the scale factor and the
volume
is multiplied by the cube of the scale factor.
2.4 Relate the changes in measurement with a
change of scale to the units used
(e.g., square inches, cubic feet) and to conversions between units (1
square
foot = 144 square inches or [1 ft2] = [144 in2], 1
cubic inch is approximately
16.38 cubic centimeters or [1 in3] = [16.38 cm3]).
3.0 Students know the Pythagorean theorem and
deepen their understanding of
plane and solid geometric shapes by constructing figures that meet given
conditions and by identifying attributes of figures:
3.1 Identify and construct basic elements of geometric figures (e.g.,
altitudes,
midpoints, diagonals, angle bisectors, and perpendicular bisectors;
central
angles, radii, diameters, and chords of circles) by using a compass and
straightedge.
3.2 Understand and use coordinate graphs to plot simple figures,
determine
lengths and areas related to them, and determine their image under
translations
and reflections.
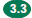 Know and
understand the Pythagorean theorem and its converse and use it Know and
understand the Pythagorean theorem and its converse and use it
to find the length of the missing side of a right triangle and the
lengths of
other line segments and, in some situations, empirically verify the
Pythagorean theorem by direct measurement.
What is the side length of an isosceles right
triangle with
hypotenuse 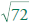 ? ?
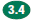 Demonstrate
an understanding of conditions that indicate two geometrical Demonstrate
an understanding of conditions that indicate two geometrical
figures are congruent and what congruence means about the relationships
between the sides and angles of the two figures.
3.5 Construct two-dimensional patterns for
three-dimensional models, such as
cylinders, prisms, and cones.
 Identify
elements of three-dimensional geometric objects (e.g., diagonals of Identify
elements of three-dimensional geometric objects (e.g., diagonals of
rectangular solids) and describe how two or more objects are related in
space
(e.g., skew lines, the possible ways three planes might intersect).
True or false? If true, give an example. If
false, explain why.
Two planes in three-dimensional space can:
1. Intersect in a line.
2. Intersect in a single point.
3. Have no intersection at all.
|
|
| |
Statistics, Data Analysis, and Probability
1.0 Students collect, organize, and represent data
sets that have one or more
variables and identify relationships among variables within a data set
by
hand and through the use of an electronic spreadsheet software program:
1.1 Know various forms of display for data sets, including a
stem-and-leaf plot
or box-and-whisker plot; use the forms to display a single set of data
or to
compare two sets of data.
1.2 Represent two numerical variables on a scatterplot and informally
describe
how the data points are distributed and any apparent relationship that
exists
between the two variables (e.g., between time spent on homework and
grade
level).
 Understand the
meaning of, and be able to compute, the minimum, the Understand the
meaning of, and be able to compute, the minimum, the
lower quartile, the median, the upper quartile, and the maximum of a
data set.
|
|
| |
Mathematical Reasoning
1.0 Students make decisions about how to approach problems:
1.1 Analyze problems by identifying relationships, distinguishing
relevant from
irrelevant information, identifying missing information, sequencing and
prioritizing information, and observing patterns.
1.2 Formulate and justify mathematical conjectures based on a general
description
of the mathematical question or problem posed.
1.3 Determine when and how to break a problem into simpler parts.
2.0 Students use strategies, skills, and concepts
in finding solutions:
2.1 Use estimation to verify the reasonableness of calculated results.
2.2 Apply strategies and results from simpler problems to more complex
problems.
2.3 Estimate unknown quantities graphically and solve for them by using
logical
reasoning and arithmetic and algebraic techniques.
2.4 Make and test conjectures by using both inductive and deductive
reasoning.
2.5 Use a variety of methods, such as words, numbers, symbols, charts,
graphs,
tables, diagrams, and models, to explain mathematical reasoning.
2.6 Express the solution clearly and logically by using the appropriate
mathematical
notation and terms and clear language; support solutions with
evidence in both verbal and symbolic work.
2.7 Indicate the relative advantages of exact and approximate solutions
to
problems and give answers to a specified degree of accuracy.
2.8 Make precise calculations and check the validity of the results from
the
context of the problem.
3.0 Students determine a solution is complete and move beyond a
particular
problem by generalizing to other situations:
3.1 Evaluate the reasonableness of the solution in the context of the
original
situation.
3.2 Note the method of deriving the solution and demonstrate a
conceptual
understanding of the derivation by solving similar problems.
3.3 Develop generalizations of the results obtained and the strategies
used and
apply them to new problem situations. |
|

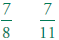
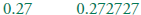
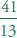 .
. Solve problems
that involve discounts, markups, commissions, and profit
Solve problems
that involve discounts, markups, commissions, and profit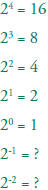
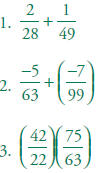
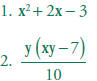
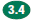 Plot the
values of quantities whose ratios are always the same (e.g., cost to
Plot the
values of quantities whose ratios are always the same (e.g., cost to Students
solve simple linear equations and inequalities over the rational
Students
solve simple linear equations and inequalities over the rational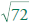 ?
? Identify
elements of three-dimensional geometric objects (e.g., diagonals of
Identify
elements of three-dimensional geometric objects (e.g., diagonals of