Adding and Subtracting Polynomials
1. Vocabulary:
• A variable is a quantity represented by a letter.
• A polynomial is the sum of terms that contain variables raised
to positive integer or zero powers and that have no variables in
any denominator .
• A term is one of the addends in an addition expression . For
example, in the expression 2x + 4, the terms are 2x and 4.
• The parts of each term that are multiplied are the factors of the
term . For example, in the term 2x from the example above, the
factors are 2 and x.
• Like terms have the same variable factors raised to the same
powers . For example, in the expression
2x^2 + 3x + 7 + 3x^2 + 4x + 9, the 2x^2 and 3x^2 are like terms, the
3x and 4x are like terms, and the 7 and 9 are like terms.
2. Adding Polynomials: To add two polynomials, use
the
commutative and associative properties of addition to rewrite the sum
so that like terms are grouped , and then use the distributive property
to combine like terms .
Example 1: Simplify.
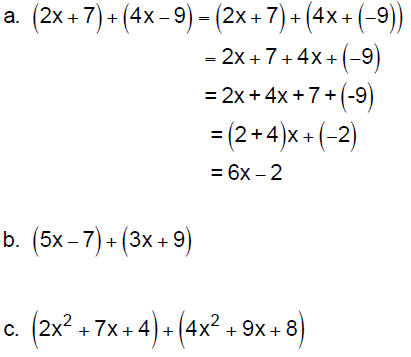
3. Negating Polynomials: If there is a negative
sign directly
preceding the parenthesis surrounding a polynomial, the negative
sign applies to each term inside the parenthesis. Use the distributive
property to distribute the negation to each term inside the
parenthesis. You may think of the negative preceding the
parenthesis as a –1, and use the rules for multiplying signed
numbers .
Example 2: Simplify.
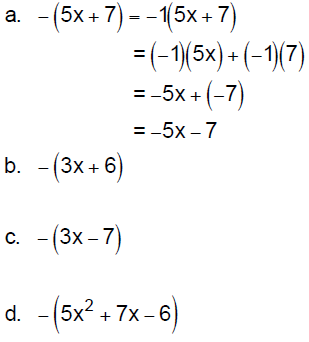
4. Subtracting Polynomials : To subtract two
polynomials, change
the subtraction to addition of the opposite and then add.
Example: Simplify.
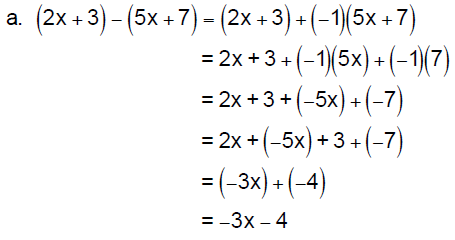
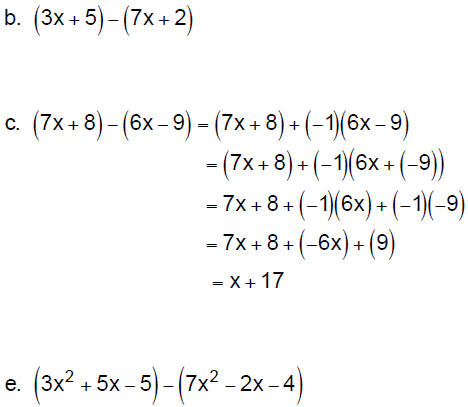
4. Evaluating Polynomials: To find the value of a
polynomial at a
given value of the variable , substitute the value of the variable into
the polynomial everywhere the variable appears.
Example: Evaluate the given polynomial at the given
value of
the variable.
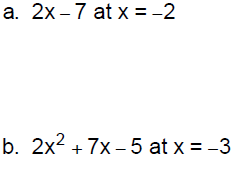
Practice Problems
Simplify each of the following :
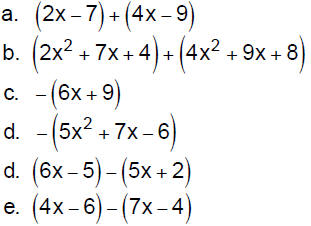
Evaluate the given polynomial at the given value of the variable.
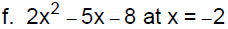
Answers to Practice Problems
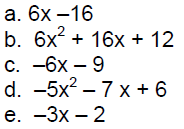
f. The value of the polynomial is 10.
| Prev | Next |