Grade 5 Math Content

Number and Operations :
Rational Numbers

The major focus of the work on rational numbers in grade 5 is on understanding
relationships among fractions, decimals, and percents. Students make comparisons and
identify equivalent fractions, decimals, and percents, and they develop strategies for
adding and subtracting fractions and decimals.

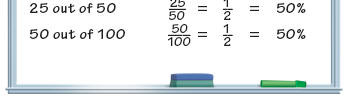
In a study of fractions and percents, students work with halves, thirds, fourths, fifths,
sixths, eighths, tenths, and twelfths. They develop strategies for finding percent
equivalents for these fractions so that they are able to move back and forth easily between
fractions and percents and choose what is most helpful in solving a particular problem,
such as finding percentages or fractions of a group.

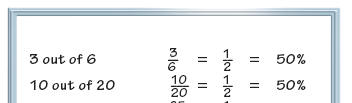
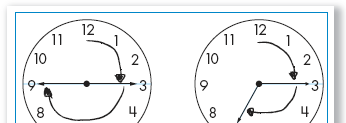
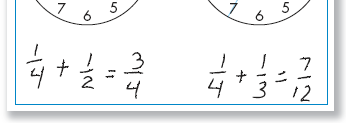
Students use their knowledge of fraction equivalents, fraction-percent equivalents, the
relationship of fractions to landmarks such as ½, 1, and 2, and other relationships to
decide which of two fractions is greater. They carry out addition and subtraction of
fractional amounts in ways that make sense to them by using representations such as
rectangles, rotation on a clock, and the number line to visualize and reason about fraction
equivalents and relationships.

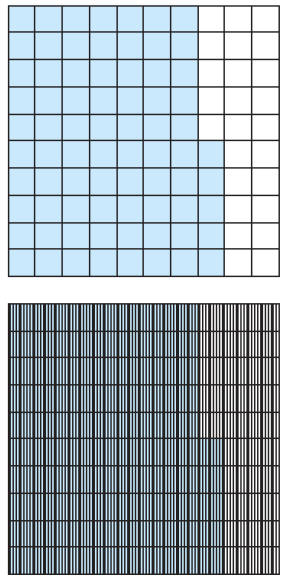
Students continue to develop their understanding of how decimal fractions represent
quantities less than 1 and extend their work with decimals to thousandths. By
representing tenths, hundredths, and thousandths on rectangular grids, students learn
about the relationships among these numbers—for example, that one tenth is equivalent
to ten hundredths and one hundredth is equivalent to ten thousandths—and how these
numbers extend the place value structure of tens that they understand from their work
with whole numbers.

Students extend their knowledge of fraction-decimal equivalents by studying how
fractions represent division and carrying out that division to find an equivalent decimal.
They compare, order, and add decimal fractions (tenths, hundredths, and thousandths) by
carefully identifying the place value of the digits in each number and using
representations to visualize the quantities represented by these numbers.

Emphases

Rational Numbers
• Understanding the meaning of fractions and percents
• Comparing fractions
• Understanding the meaning of decimal fractions
• Comparing decimal fractions

Computation with Rational Numbers
• Adding and subtracting fractions
• Adding decimals

Benchmarks

• Use fraction-percent equivalents to solve problems about the percentage of a
quantity
• Order fractions with like and unlike denominators
• Add fractions through reasoning about fraction equivalents and relationships
• Read, write, and interpret decimal fractions to thousandths
• Order decimals to the thousandths
• Add decimal fractions through reasoning about place value, equivalents, and
representations

Patterns, Functions, and Change

In Grade 5, students continue their work from Grades 3 and 4 by examining,
representing, and describing situations in which the rate of change is constant . Students
create tables and graphs to represent the relationship between two variables in a variety of
contexts. They also articulate general rules for each situation. For example, consider the
perimeters of the following set of rectangles made from rows of tiles with three tiles in
each row:

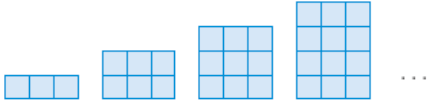
If the value of one variable (the number of rows of three tiles) is known, the
corresponding value of the other variable (the perimeter of the rectangle) can be
calculated . Students express these rules in words and then in symbolic notation. For
example:

For the first time in Grade 5, students create graphs for situations in which the rate of
change is itself changing–for example, the change in the area of a square as a side
increases by a constant increment–and consider why the shape of the graph is not a
straight line as it is for situations with a constant rate of change.

Throughout their work, students move among tables, graphs, and equations and between
those representations and the situation they represent. Their work with symbolic notation
is closely related to the context in which they are working. By moving back and forth

between the contexts, their own ways of describing general rules in words, and symbolic
notation, students learn how this notation can carry mathematical meaning .

Emphases

Using Tables and Graphs
• Using graphs to represent change
• Using tables to represent change

Linear Change
• Describing and representing a constant rate of change

Number Sequences
• Describing and representing situations in which the rate of change is not constant

Benchmarks

• Connect tables and graphs to represent the relationship between two variables
• Use tables and graphs to compare two situations with constant rates of change
• Use symbolic notation to represent the value of one variable in terms of another
variable in situations with constant rates of change

Data Analysis and Probability

Students continue to develop their understanding of data analysis in Grade 5 by
collecting, representing, describing, and interpreting numerical data . Students’ work in
this unit focuses on comparing two sets of data collected from experiments. Students
develop a question to compare two groups, objects, or conditions. (Sample questions:
Which toy car goes farthest after rolling down the ramp? Which paper bridge holds more
weight?). They consider how to ensure a consistent procedure for their experiment and
discuss the importance of multiple trials . Using representations of data, including line
plots and bar graphs, students describe the shape of the data—where the data are
concentrated, how they are spread across the range. They summarize the data for each
group or object or condition and use these summaries, including medians, to back up their
conclusions and arguments. By carrying out a complete data investigation, from
formulating a question through drawing conclusions from their data, students gain an
understanding of data analysis as a tool for learning about the world.

In their work with probability, students describe and predict the likelihood of events and
compare theoretical probabilities with actual outcomes of many trials. They use fractions
to express the probabilities of the possible outcomes (e.g., landing on the green part of the
spinner, landing on the white part of the spinner). Then they conduct experiments to see
what actually occurs. The experiments lead to questions about theoretical and

experimental probability, for example, if half the area of a spinner is colored green and
half is colored white, why doesn’t the spinner land on green exactly half the time?

Emphases
Data Analysis
• Representing data
• Describing, summarizing, and comparing data
• Analyzing and interpreting data
• Designing and carrying out a data investigation

Probability
• Describing the probability of an event
• Describe major features of a set of data represented in a line plot or bar graph, and
quantify the description by using medians or fractional parts of the data

Benchmarks

• Draw conclusions about how 2 groups compare based on summarizing the data
for each group
• Design and carry out an experiment in order to compare two groups
• Use a decimal, fraction, or percent to describe and compare the theoretical
probabilities of events with a certain number of equally likely outcomes

Geometry and Measurement

In their work with geometry and measurement in grade 5, students further develop their
understanding of the attributes of two-dimensional (2-D) shapes, find the measure of
angles of polygons, determine the volume of three-dimensional (3-D) shapes, and work
with area and perimeter. Students examine the characteristics of polygons, including a
variety of triangles, quadrilaterals, and regular polygons. They consider questions about
the classification of geometric figures, for example:

Are all squares rectangles?

Are all rectangles parallelograms?

If all squares are rhombuses, then are all rhombuses squares?

They investigate angle sizes in a set of polygons and measure angles of 30, 45, 60, 90,
120, and 150 degrees by comparing the angles of these shapes. Students also investigate
perimeter and area. They consider how changes to the shape of a rectangle can affect one
of the measures and not the other (e.g., two shapes that have the same area don’t
necessarily have the same perimeter), and examine the relationship between area and
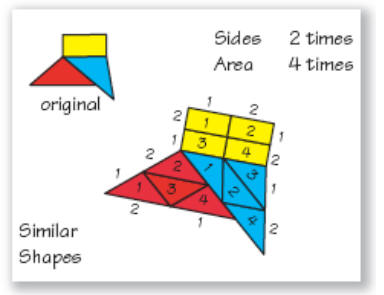
perimeter in similar figures.

Students continue to develop their visualization skills and their understanding of the
relationship between 2-D pictures and the 3-D objects they represent. Students determine
the volume of boxes (rectangular prisms) made from 2-D patterns and create patterns for
boxes to hold a certain number of cubes. They develop strategies for determining the
number of cubes in 3-D arrays by mentally organizing the cubes—for example as a stack
of three rectangular layers, each three by four cubes. Students deepen their understanding
of the relationship between volume and the linear dimensions of length, width, and
height. Once students have developed viable strategies for finding the volume of
rectangular prisms, they extend their understanding of volume to other solids such as
pyramids, cylinders, and cones, measured in cubic units.

Emphases

Features of Shape
• Describing and classifying 2-D figures
• Describing and measuring angles
• Creating and describing similar shapes
• Translating between 2-D and 3-D shapes

Linear and Area Measurement
• Finding the perimeter and area of rectangles

Volume
• Structuring rectangular prisms and determining their volume
• Structuring prisms, pyramids, cylinders, and cones and determining their volume

Benchmarks

• Identify different quadrilaterals by attribute, and know that some quadrilaterals
can be classified in more than one way
• Use known angle sizes to determine the sizes of other angles (30 degrees, 45
degrees, 60 degrees, 90 degrees, 120 degrees, and 150 degrees)
• Determine the perimeter and area of rectangles
• Identify mathematically similar polygons
• Find the volume of rectangular prisms
• Use standard units to measure volume
• Identify how the dimensions of a box change when the volume is changed
• Explain the relationship between the volumes of prisms and pyramids with the
same base and height