Solutions to Algebra I Problem Set 5
1. We need to show that if G is a finite abelian group , and
if f : G → K is a surjective
homomorphism to an abelian group K , then G has a subgroup which is isomorphic
to K. (If we let K = G/H we get the desired result).
Since G is a finite abelian group , there are integers
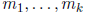each a power of a
prime number such that
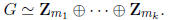
By putting the summand which corresponds to the same prime number, we can
assume that
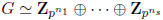
for a prime number p and integers
.
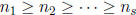Then we can write K as
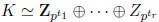
such that
.
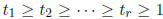To prove the statement, it is enough to show that
for every
.
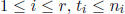Assume on the contrary that this is not true, and assume
that l is the largest index for which
.
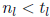For
,
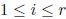let
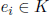be the element
whose summands are all zero expect a 1 at the i-th place (0,... , 1, ... ,
0), and for
,
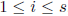let 
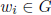be the element whose summands are all zero except a 1 at the
i-th place.
For
,
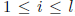let
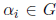be such that
.
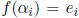Then let
.
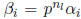Then
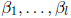are in the subgroup of G generated by
,
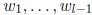and so the same is true
for their images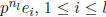 
:
They are in the subgroup generated by l-1 elements
.
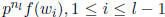This is a contradiction since none of the
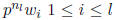are
zero .
2. Assume that H is a finite subgroup of Q/Z. First note that if
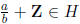where
gcd(a, b) = 1, then
:
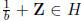since gcd(a, b) = 1, there are integers x and y such
that ax + by = 1, so
.
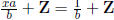Now let Let now
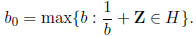
Then H is the cyclic group generated by
:
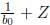if
,
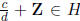then so is
.
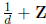Let now a = gcd(d,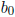 
). Then there are integers x and y such that
.
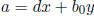So
.
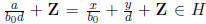But
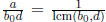, and since
,
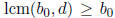by our
choice of 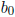, lcm (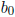, d) should be equal to
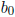, so d is a divisor of
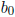, and
.
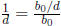So
H is cyclic and its order is .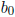
Therefore, the only subgroup of Q/Z is the subgroup generated by
.
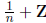3. Assume R is commutative and let I be the set of nilpotent elements. To show
that
R is an ideal, we need to show that
•
For a, b ∈ I, a + b ∈ I: If an = 0 and bm = 0, then (a + b)nm = 0.
•
For a ∈ I, -a ∈ I: If an = 0, then (-a)n = -an = 0.
•
For a ∈ I and r∈ R: ra ∈ I: If an = 0, then (ra)=rnan = 0.
If R is not commutative, then I is not necessarily an ideal: Let R the ring of 2
by 2 matrices with real entries . Then
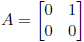and
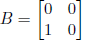are nilpotent, but
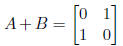which is not nilpotent as
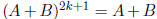and
.
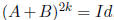4.
(i) In this case,
.
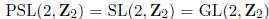The isomorphism is give by
,
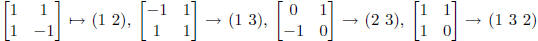and
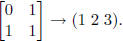
(ii) The isomorphism is given by
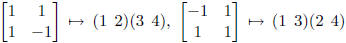
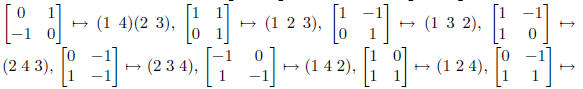
(1 3 4), and
.
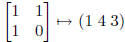5. (b) Assume G is not cyclic. It is enough to consider the case where H is of
the form
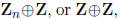or
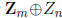where m and n are not relatively prime. In the third case,
define Ø: G → G by
,
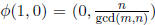and Ø(0, 1) = (0, 1). Define
:
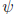G →G
by
.
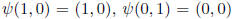Then
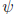and Ø extend to homomorphisms of G.
And we have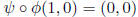
and
.
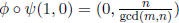Hence End(G) is not
commutative.
In the other two cases , similar Ø and
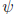work.
| Prev | Next |