Solutions to Math 1155 Exam 2 Solutions
Solutions to Exam 2
This was a tougher exam than the first one. Some of that had to do with the
material;
Chapter 3 is harder than Chapter 2. If you felt like you studied a lot more for
this exam than for exam 1, but didn’t do as well as you’d like, come talk to me.
I
might be able to give you suggestions about how to study for an exam in this
class.
(I know it sounds silly, but it can help.)
Note: After each problem I’ve tried to indicate how likely
it is to show up again on
the final exam, perhaps slightly modified. There are no guarantees, but because
I’m
writing the final exam, chances are pretty good that I know what will be on
it...
If you can’t figure out why a given answer is correct,
talk to us after class or in office
hours.
1. (i) B. This is the Remainder Theorem. The remainder
after dividing f (x) by
(x − c) is f(c). In this case that means f(2) is 1. (Will almost certainly
return in
the multiple choice section of the final exam.)
(ii) D. To check the number of negative real roots, we
need to examine f(−x):
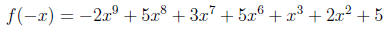
There is only one change of sign here , so there is exactly
one negative real root. (The
multiple choice section of the final exam will most likely have a question
involving
Descartes’ Rule of Signs.)
(iii) C.
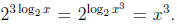 (The final exam will include some problem(s) where
(The final exam will include some problem(s) where
you have to manipulate logs and exponents , although it might not look exactly
like
this.)
(iv) A. For very large values , R(x) behaves like
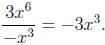
(You’ll have to know something about the end behavior of polynomials and
rational
functions for the final.)
2. This problem, or something very, very similar, will be on the final exam.
(i) Using the Rational Zeros Theorem, any rational zeros
(or rational “roots,” if you
prefer) must be of the form ±p/q, where p is a factor of 3 and q is a factor of
2.
There are the following possibilities:
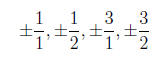
(ii) The degreee of f(x) is 4, so there are at most 4 real
roots . Using Descartes’ Rule
of Signs, there are no positive roots, and 4, 2, or 0 negative roots. This helps
us in
part (iii) because you don’t have to bother checking the positive numbers we
listed
above. We only need to check the negative ones.
(iii) Checking only the negative roots from the list in (i),
we find that x = −1 and
x = −1/2 are roots; in other words, (x +1) and (x +1/2) are factors of f(x).
Using
synthetic division or long division, you can find that
f(x) = (x + 1)(x + 1/2)(2x2 + 6)
We’re only halfway done; (2x2 + 6) doesn’t have any real
roots, but we’re supposed
to find all complex roots , and (2x2 + 6) = 0 whenever x2 = −3, or
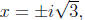 where
where
i is the imaginary number
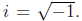 (If you don’t believe that works, check it by
(If you don’t believe that works, check it by
solving 2x2 +6 = 0 with the quadratic formula!) In all of its final factored
glory, the
polynomial is
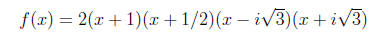
3. (i) The key to this problem is to write each side as 5
to some exponent:
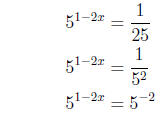
Equating exponents, we have
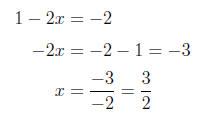
(ii) Here we use the following properties of logarithms :
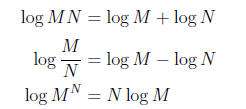
In the particular case of the monstrosity on the exam:
log
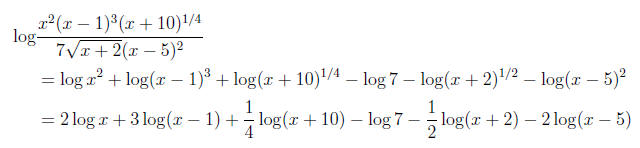
(Problems similar to (i) and (ii) could show up on the
final exam. In particular, the
techniques in (ii) are useful for certain problems in calculus, so we want to
make
sure you learn them now.)
4. To find the inverse function, we solve for x :
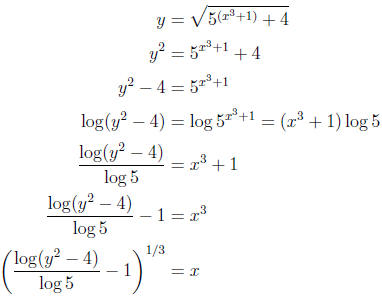
Finally, following our convention, we switch x and y:
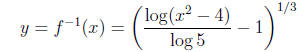
Note that your answer might look different , depending on
whether you used log, ln,
log5, and so on. (You might have to find an inverse function on the final exam,
but
I’ll try to stay away from logs and exponential functions.)
5. Ask us about this problem in person if you’re not sure
how it went. On the final
exam, you’ll either be given a rational function and asked to sketch its graph ,
or
vice-versa.)
| Prev | Next |